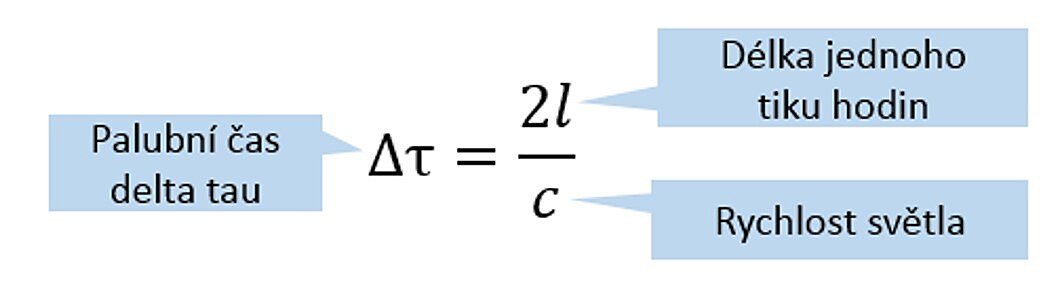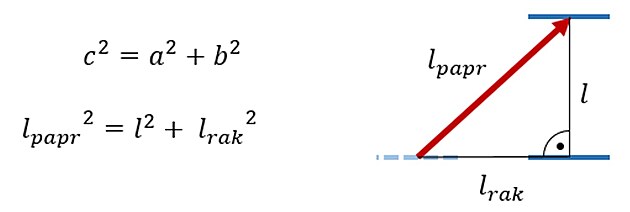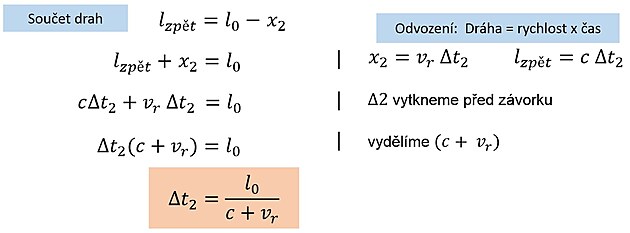Povídání o nekonečnu 7. část - Speciální teorie relativity

Ve svém povídání se pomalu přesunuji do reálného světa. Ve Speciální Teorii Relativity nacházíme nekonečnost v limitním přibližování se rychlosti světla. I přes svou důmyslnost není tato teorie bez výtek či námitek.

Zřejmě všichni známe pojem dilatace neboli natahování času, který v době Einsteinovy první prezentace otřásl základy zažitých představ a samozřejmě se setkal s obecným nepochopením. Čas se z určitého hlediska může jevit jako veličina pouze zdánlivá, která je pouze mírou změny ve vzájemném (relativním) pohybu objektů. 

Vesmír je plný objektů – jednotlivých a hromadných. Za nejmenší jednotlivé objekty ve Speciální Teorii Relativity (dále jen STR) považujeme fotony. (Ve skutečnosti si nejsme jisti tj. nevíme, zdali existují menší). Takže většinu objektů vyjma prvotních elementárních částic můžeme považovat za hromadné s různým stupněm hromadnosti – složitosti.

Každý takovýto objekt chápeme jako soustavu, která je ve vztahu tj. v relaci k jinému objektu neboli soustavě a dohromady tak tvoří soustavu další.

Objekty – soustavy se vůči sobě pohybují různými rychlostmi. Pokud chceme rychlost měřit, musíme zvolit stanoviště pozorovatele, potom však veškeré údaje budou v relaci k tomuto stanovišti, tj. subjektivní. Protože jsme nedílnou součástí pohybujících se soustav, nejsme schopni nalézt nějaké absolutně klidové stanoviště, vůči kterému by se vše ostatní pohybovalo objektivně. (Pokud na vedlejší koleji jede vlak stejnou rychlostí, máme dojem, že stojí, na druhé straně ubíhá krajina, jak popisujeme svůj vjem. Bez předchozích poznatků nejsme schopni rozlišit, kdo se pohybuje, my nebo krajina. Pokud narazí jedoucí vlak do stojícího, účinek je pro oba stejný).

Co je tedy dilatace (natahování) času podle STR?

Podle STR se světlo (z vlnového hlediska elektromagnetické vlnění - EM, z kvantového částice zvané fotony) pohybuje neměnnou konstantní rychlostí, tzn. žádná rychlost se k němu nepřičítá ani neodečítá, pouze se natahuje nebo zkracuje jeho vlna v závislosti zda opouští objekt v protisměru nebo ve směru jeho pohybu (Dopplerův efekt).

Fotony jako tzv.intermediální částice mají na svědomí elektronové vazby a tím pádem soudržnost hmoty složené z atomů tj. těžké (baryonové) hmoty, ze které jsou složeny viditelné objekty našeho vesmíru včetně nás.

Pokud se objekt (soustava) pohybuje pomalu, dojde k výměně fotonů v jeho struktuře velmi rychle. Naopak čím víc se daná struktura blíží k rychlosti světla, tím déle trvá než foton vyslaný z atomu dorazí k atomu, který letí vedle něj, který mu obrazně řečeno „ujíždí“, takže musí letět po delší šikmé dráze. Světočára tohoto fotonu je delší. To znamená, že se zpomalí proces výměny energií a informací mezi jednotlivými atomy, potažmo molekulami a vlastně se tím zpomalí proces zrání celého objektu (soustavy).

Dilatace času je ve skutečnosti pouhé prodlužování dráhy částic uskutečňujících interakci mezi objekty. (Interakce chápeme jako vzájemné silové působení a výměnu informací způsobující vázání, vznik, zrání a rozpad objektů). Toto líčení je však jednostranné.

Pro demonstraci problematiky je asi nejznámější obrazný pokus se stále pomaleji stárnoucím kosmonautem, který letí v raketě přibližující se rychlosti světla. Tento příklad nacházíme v různém stupni jasnosti vysvětlení. Pokusme se také o jeden (lidovější).

Dilatace

Nejdříve si řekněme nějaké vstupní informace, ze kterých budeme vycházet. V raketě jsou světelné hodiny složené ze dvou zrcadel (A, B) vzdálených od sebe délkou l (l jako longitudo, length - délka) a umístěných kolmo na směr pohybu rakety. Jeden hodinový tik rovná se letu paprsku ze zrcadla A do zrcadla B a zpět čili 2krát délka l  (2l)

Palubní čas, který si označíme „delta Tau“, se vypočítá  pomocí vzorce

který jsme odvodily od základního vzorce pro výpočet rychlosti jako dráhy (vzdálenosti dvou bodů) za čas (vpravo úpravy vzorce pro výpočet dráhy s a času t).

Palubní čas se z hlediska kosmonauta v raketě po celou cestu nemění. Kosmonaut své okolí pozoruje a zaznamenává z hlediska palubních hodin. Rozdíl se projeví až po přistání zpět na zemi. Hodiny v raketě šly pomaleji. Proč? Dopředu můžeme říct, protože dráha paprsku určující jedno tiknutí (kmit) hodin byla v raketě delší než na zemi. Hodiny stačily tiknout méně krát.

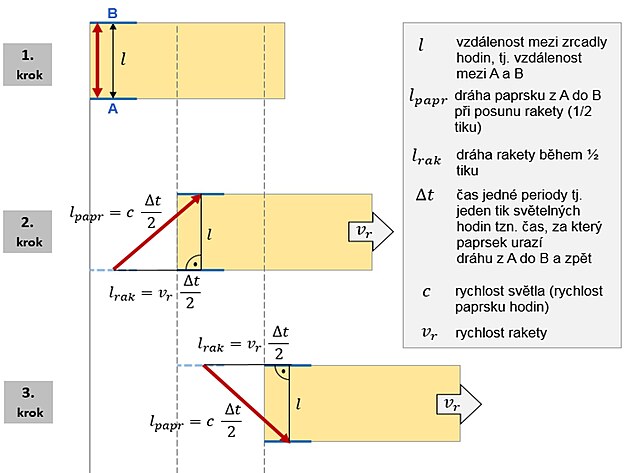
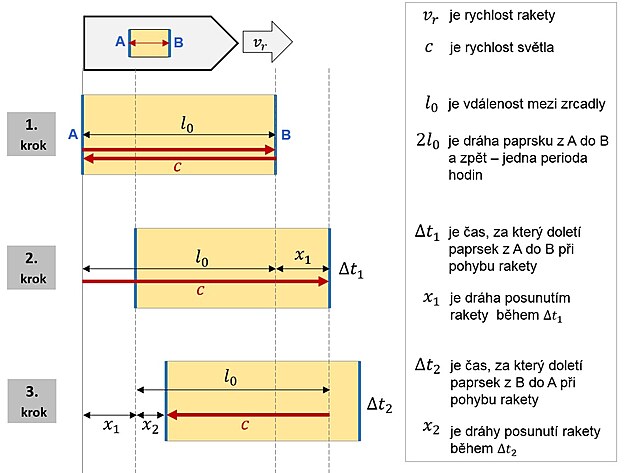
Let čili posun rakety si rozdělíme do tří kroků (popis pod obrázkem).

1. krok  -  Raketa stojí na Zemi, pro porovnání časů považujeme stav na Zemi za klidový a paprsek světla běhající mezi zrcadly za kolmý. Palubní čas je shodný s časem na Zemi a vypočítáme ho podle výše uvedeného vzorce.

2. krok  -  Raketa letí určitou rychlostí, tato rychlost je rychlost oproti zemi, neboť na Zemi jsme výchozí rychlost rakety určili jako nulovou. Pokud se raketa pohybuje, zrcadlo B ujíždí a dráha paprsku se tak prodlužuje.

Dráha paprsku z A do B (jeden půl-kmit hodin), se pak rovná  rychlost světla c  krát doba půlky periody hodin(?t)/2   tj. čas, za který dorazí paprsek z A do B

Dráha posunutí rakety během doby, kterou potřebuje paprsek z A do B, se rovná  rychlost rakety v (s indexem r) krát doba půlky periody hodin (?t)/2

3. krok - Při návratu paprsku k zrcadlu A se děj symetricky opakuje, raketa se posune o stejný kus jako při 2. kroku, doba i dráha paprsku jsou stejné jako při cestě k zrcadlu B, proto nemusíme časy rozlišovat a můžeme použít  (?t)/2.

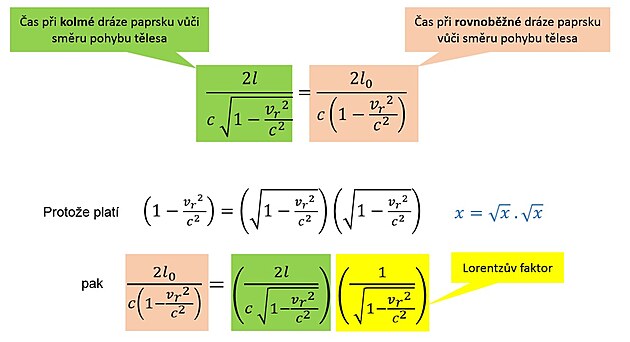
Nyní ze vzniklé situace potřebuje odvodit čas ?t  (čas pozorovatele na Zemi), který je předmětem našeho hledání. Hodnoty tvoří pravoúhlý trojúhelník, takže můžeme použít Pythagorovu větu...              

... a rovnici začít upravovat. Popsaná úprava se projeví na dalším řádku. Modře je zmíněno pravidlo, dle kterého se upravuje.

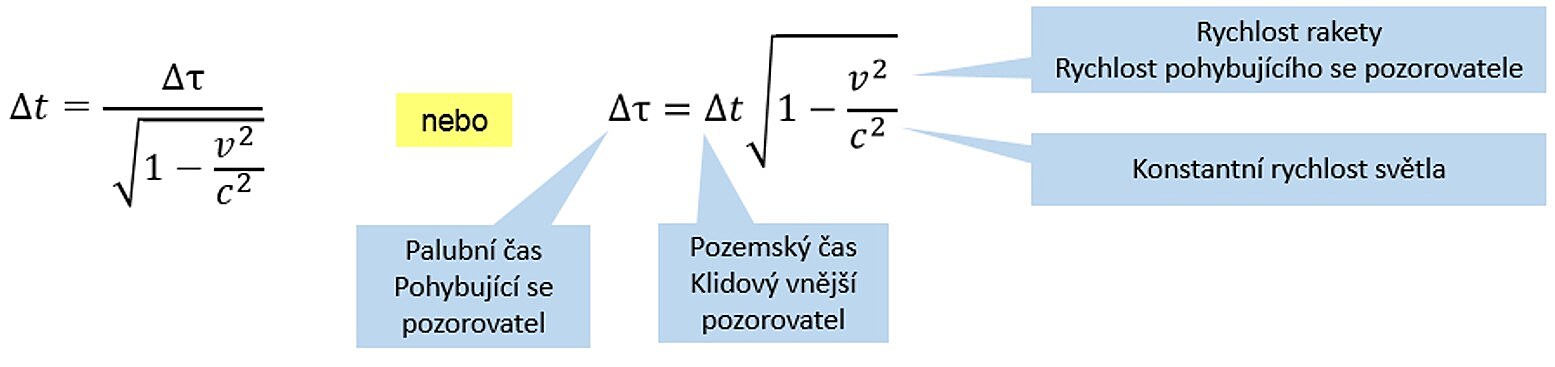
A dostáváme výsledný dilatační vzorec. Rychlost rakety zobecníme z v (s indexem r)  na samotné v, tedy na rychlost jakéhokoli objektu nebo soustavy.

Pokud raketa bude v relativním klidu tj. bude se pohybovat synchronně se soustavou vnějšího pozorovatele dosadíme v = 0 , pak jmenovatel ve zlomku = 1 a platí ?t = ??.

Za 10 let kosmonaut při třetí kosmické rychlosti ušetří půl sekundy. To není zrovna moc. Můžeme vzít poloviční rychlost světla 149 896 229 m/s, kterou letí loď ve filmu Pasažéři.

A našemu pasažéru za 10 pozemských let (v nehibernovaném stavu) palubní hodiny ukáží 273291221 sekund neboli 8,66 roku. Ušetří jeden a čtvrt roku.

Pokud by letěl 90% rychlostí světla, palubní hodiny ukáží 137553564.73 sekund neboli 4,36 roku. Kosmonaut ušetří necelých 6 let

95%     98536551.03 sekund   3,12 roku   - ušetří necelých 7 let          

99%     44516559.02 sekund   1,41 roku   - ušetří přes 8 a půl roku

99,9%  14109169.35 sekund   0,45 roku   - ušetří přes 9 a půl roku

Z toho je patrné, že skutečný nárůst ušetřených let vzniká až při limitně těsném přibližování se rychlosti světla. 

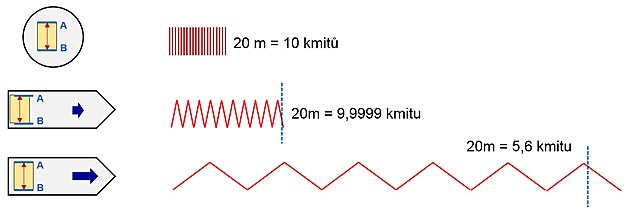
V přehledu si nakreslíme zjednodušené (bez souřadnic) světočáry (tj. dráhy v prostoru a čase) paprsků hodin při různých rychlostech. (AB = 1 m). Vidíme, že jediné co se natahuje, je dráha paprsku, který při zvyšující se rychlosti stačí za uraženou stejnou vzdálenost provést méně kmitů - tiků. (Tiky na Zemi /kruh/ jsem pro přehlednost nakreslil vedle sebe).  

Co jsme zjistili s jistotou, je, že světelné hodiny se budou se vzrůstající rychlostí zpomalovat.

Jak to ale bude s hodinami mechanickými nebo biologickými? Bude organismus skutečně stárnout pomaleji?

Uvažuje se tak, že v základu biologických dějů stojí děje chemické, v základu chemických kvantově mechanické. Jak už bylo výše řečeno, molekuly potažmo atomy a jejich elektrony na sebe reagují (interagují) pomocí fotonů. Předpokládá se, že pokud bude docházet ke zpoždění interakcí (k výměně informací), bude se zpomalovat celý děj vývoje a zrání. To platí i pro mechaniku neorganických těles (= delší poločasy rozpadů). Prostě čím vyšší rychlost, tím více děj bude připomínat zpomalený film. Kosmonaut, co se týče náplně života vlastně nic neušetří, protože toho také méně stihne prožít. Pokud bude pozorovat život na Zemi, bude mu připadat zrychlený. Pokud by si pořídil záznam, stejně si ho pro zpracování musí zpomalit do své rychlosti.

Při 100% rychlosti by se měl čas, tedy veškeré interakce způsobující vývoj a stárnutí zastavit, protože zprostředkující fotony by nemohly dostihnout vedlejší částici ve struktuře. Vlastně by taková raketa ani nemohla opět zpomalit, protože ve vakuu bez odporu prostředí by nebyl k dispozici mechanismus, který by spustil jakoukoli brzdící funkci. Celý letící objekt by zamrzl v okamžiku odsouzen k věčnému letu.

Kontrakce

Dalším relativistickým jevem je tzv. kontrakce (zkracování) délek

Na palubě rakety jsou světelné hodiny složené ze dvou zrcadel umístěné rovnoběžně se směrem pohybu rakety.

Jedna perioda tj. jedno tiknutí hodin je let paprsku ze zrcadla A do zrcadla B a zpět.

1. KROK 

Pokud je raketa v klidu, dráha paprsku při cestě tam i zpět je stejná, rovněž potřebný čas. (Vzorec je odvozen od základního vztahu vpravo)

2. KROK

Pokud raketa letí určitou rychlostí ve směru paprsku, musí paprsek urazit delší vzdálenost a za delší dobu, než když je raketa v klidu.

3. KROK

Paprsek při cestě zpět letí proti pohybu rakety, dráhu mezi zrcadly urazí dříve, takže raketa stačí urazit menší vzdálenost než při letu paprsku mezi zrcadly ve směru rakety. (Čím větší rychlost rakety, tím větší nerovnost x1 > x2).

Sečtením obou časů dostaneme čas, za který paprsek doletí z A do B a zpět tj. tik hodin.

Délka pro pozorovatele ze směru kolmého na směr pohybu tělesa zůstává nedotčena.

(Tolik školní vědomosti, dále vlastní úvahy).

Námitky

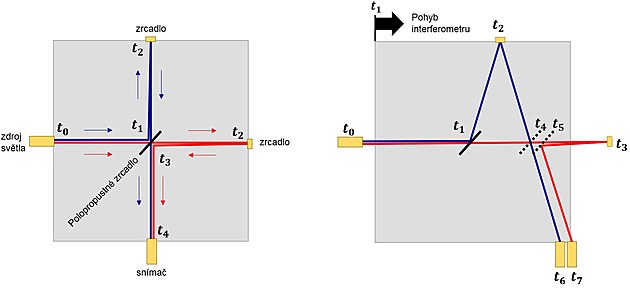
Výchozím bodem Teorie relativity pro Alberta Einsteina byl experiment pánů Michelsona a Morleyho, kteří se snažili dokázat existenci éteru a z jeho výsledku odvozené tzv. Lorentzovy transformace. Na základě hypotézy, že éter je nějaká řídká a v celém vesmíru nepohyblivá substance, která by na pohyb těles relativně působila jako vítr (táhnete-li rukou po klidné hladině vody, pociťujete odpor, jako by voda proudila), sestrojili přístroj zvaný Interferometr, který zahrnuje dvě na sebe kolmé stejně dlouhé dráhy, a který by při pohybu přístroje (společně se Zemí) musel vykazovat zpoždění paprsku na dráze rovnoběžné se směrem pohybu způsobený zdánlivým protiproudem. (Nespolečné části drah přístroje odpovídají výše uvedeným polohám světelných hodin – první kolmá /modrá/ při dilataci, druhá rovnoběžná /červená/při kontrakci).

Jenže při pokusu interferometr nevykazoval mezi drahami žádné rozdíly, vše probíhalo, jako by Země byla v klidu. To vedlo Hendrika Lorentze k myšlence zkrácení tělesa ve směru jeho pohybu a zavedení Lorentzova faktoru, který rozdíl kompenzuje a to stále ještě v představě své éterové teorie, kde světlo je vlnění předávané mediem, podobně jako zvuk nebo vodní vlna.

Albert Einstein následně odmítl éter a zavedl myšlenku nezávislých světelných částic volně letících konstantní rychlostí vakuem. Tím se však na problematice rozdílu drah při pohybu v zásadě nic nezměnilo. Protiproud byl nahrazen konstantní rychlostí a rozdíl drah při pohybu tělesa by tak jako tak musel být buď patrný nebo požadující zkrácení. Nyní je důležité, v jakých souvislostech budeme o zkrácení uvažovat.

(Nyní prosím o trpělivost s vylíčení všech tj. také chybných aspektů, kde se nevyhnu jisté kostrbatosti a opakování). Výše ve školním výkladu se hovoří o zkrácení vzhledem vzdálenému relativně klidovému pozorovateli, přičemž pozorovatel ze směru kolmém na pohyb tělesa žádné zkrácení nepozoruje. Z toho by mělo vyplývat, že nedochází ke skutečnému zkrácení vlastního tělesa, ale pouze ke zkrácení obrazu tělesa, který je přijat vzdáleným relativně klidovým pozorovatelem, od kterého se těleso vzdaluje.

Pokud by ale nedocházelo k vlastnímu zkrácení, musel by interferometr zaznamenat rozdíl mezi drahami, neboť tyto by měly být při pohybu různě dlouhé. Jenže, jak už bylo řečeno, interferometr, přesněji světlo, pokud ho vysíláme a přijímáme v téže soustavě, se chová jako by soustava byla v klidu. To zřejmě vedlo Alberta Einsteina k myšlence volitelné vzájemné relativity všech těles pohybujících se ve vakuu nezávisle na nějakém pozadí. A opět jenže:

Když budeme uvažovat o každém tělese, jako o autonomním systému, který je vůči světlu v klidu a rychlost spolu s deformací přijímaného obrazu z okolí se projeví až ve vztahu k jinému tělesu, pak by se fotony v každé soustavě musely pohybovat jinou rychlostí.  (Mohla by tak existovat vzájemně velmi vzdálená tělesa vůči sobě se pohybující nadsvětelnými rychlostmi). Znamenalo by to také, že všechny paprsky opouštějící svá tělesa by byla bez spektrálního posuvu a posuv by se projevil až při přijetí paprsku jiným tělesem.

Problémem by pak bylo, že dilatační efekt pomalého stárnutí by měl být také oboustranně relativní, tj. bylo by jedno, jestli opouští raketa Zemi nebo Země raketu a z pohledu rakety by se vrátil pozemšťan a měl by být oproti kosmonautovi mladší, což je těžký spor. Teorie relativity ale počítá s rychlostním stropem pro všechny (Postulát rychlosti světla). Světlo se podle ní pohybuje ve všech soustavách stejně rychle, uvnitř těles i mezi tělesy.

Proto se intuitivně uvažuje o vesmíru jako o poli (vlnoploše), v němž informační síť propojenou všemi směry obstarává světlo. Tato síť má nastavenou pracovní rychlost a všechny objekty pohybující se v této síti jsou buď více či méně pomalejší od její pracovní rychlosti a je samozřejmě jedno, jakým směrem se pohybují. To logicky předpokládá nulovou rychlost vůči rychlosti světla (stav, kdy ve světelných hodinách paprsek urazí nejmenší možnou dráhu v porovnání s jakoukoli jinou soustavou) a jedná se vlastně o základní vztažnou soustavu vůči všem tělesům. Pak ale nelze hovořit o absolutní relativitě. Pokud se ale rychlosti těles poměřují s rychlostí světla jako takové sami o sobě, musel by interferometr naměřit rozdíl mezi drahami, protože tyto při pohybu tělesa nejsou stejně dlouhé a k vyrovnání by muselo docházet ke skutečnému zkrácení (Lorentzem zřejmě uvažované), které by ale zase muselo být pozorovatelné i pro pozorovatele ze strany kolmé na směr pohybu tělesa, a o kterém se tvrdí, že pozorovatelné není. Nelze si tedy hrát na klidový stav jen proto, že nás nikdo jiný nepozoruje, a začít si hrát na přibližování se k rychlosti světla, až když se začneme vztahovat k jiné soustavě.

Ještě jednou přehled ve zkratce.

-  c je společné pro všechny soustavy, interfer. nenaměří rozdíl drah při skutečném zkrácení, které ale musí být viditelné ze strany.

-  autonomní soustavy, interfer. nenaměří rozdíl, zkrácení je zdánlivé a neviditelné ze strany, c pak nemůže být společné pro všechny soustavy.

-  pomalejší stárnutí rychlejšího předpokládá absolutní pořadí rychlostí, které platí pro všechny, což se rovná hromadné vztažné soustavě.

Prostě pokud vezmeme STR jako soustavu tvrzení, tak alespoň některé z nich nemůže platit, nahlédneme-li na všechna v jediném obraze.

Představte si případ dvou vůči sobě se pohybujících objektů (bez skutečného zkrácení), na kterých jsou umístěné interferometry. Kdyby na obou interferometry naměřily stejné dráhy, musely by se rychlosti světla k rychlostem objektů přičítat. Kdyby se objekty zkracovaly sami o sobě pouze poměrem své rychlosti vůči světlu, muselo by jejich zkrácení být patrné všem okolním pozorovatelům. Muselo by vlastně docházet k dvojí úpravě délky. K vlastnímu zkrácení vlastní rychlostí a pak ke zkrácení nebo natažení (viz níže) relativní rychlostí vůči objektu, se kterým tvoří vztažnou soustavu.

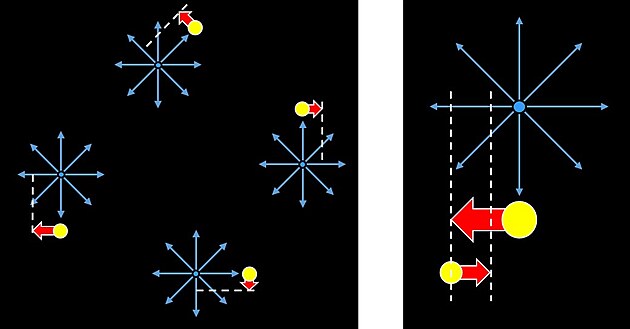
(Vsuvka) Nemá to nic společného se spektrálním posuvem. Ten skutečně ukazuje pouze vzájemnou rychlost. Zde na zemi nám ukáže, jakou relativní rychlostí se pohybujeme vůči objektům v našem obzoru. Pro úplnost doplním základní info:

Posuv čar ve spektru pozorovaného světla má na svědomí Dopplerův efekt. Pokud si foton představíme zároveň jako vlnu světla připomínající pružinu, pak se vlna prodlužuje nebo zkracuje podle toho, zdali je v průběhu opouštění „mateřské“ částice tlačena po směru nebo natahována v protisměru jejího pohybu.

Obr. níže:

Nahoře: vzdalující se objekt od klidového - efekt je pro oba stejný, nelze určit, který se vzdaluje.

Dole: oba objekty se pohybují stejným směrem a rychlosti - efekt je stejný jako v klidovém stavu.  

Je mi také trochu divné, že se všude hovoří pouze o zkracování (kontrakci) a nikdy o prodlužování a všude se uvažuje pouze v mínusech vyjma zpětného převodu do původní vztažné soustavy. Lorentzovy transformace jsou odvozeny z postulátu o konstantní rychlosti světla ve všech soustavách, obsahují jeden Lorentzův faktor, který udává natažení času a zkrácení délky pouze na základě relativní rychlosti a vůbec nedává (tedy mně nedává, abych případně negeneralizoval svou blbost) odpověď na výše uvedené otázky, neboť uvedený spor předpokládá i možnost, že by postulát nemusel platit nebo být ještě jinak podmíněný či vymezený na určitý okruh událostí.

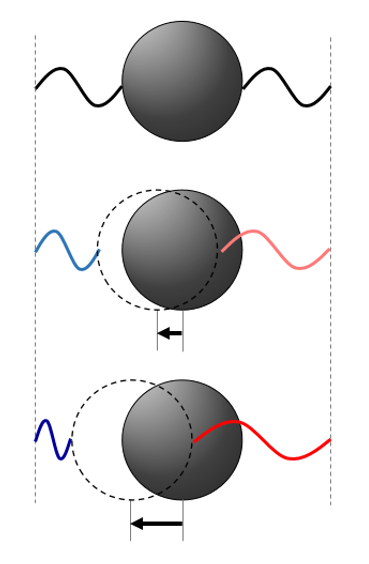
Níže uvádím intuitivní obrázky, kde se obraz pozorovaného objektu zkracuje nebo prodlužuje dle toho, zda se vzdaluje nebo přibližuje a kde úprava délky je pouze relativní. 

Vzdálená vesmírná tělesa pozorujeme opticky (např.Hubble telescope), radiově nebo pomocí rentgenových paprsků (např.Chandra telescope). Tato pozorování jsou pasivní, zaznamenávají pouze cestu světla k nám. (Kdybychom chtěli něco vysílat a čekali na návrat, to bychom se načekali).

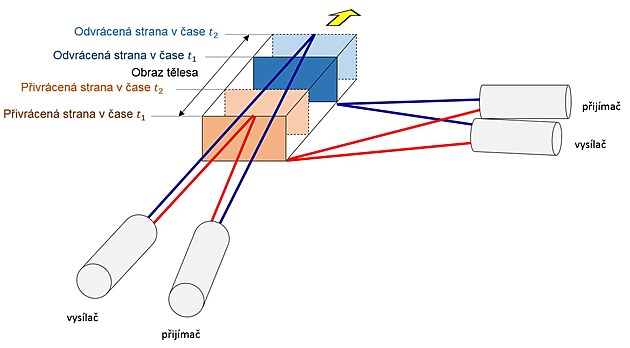
Uvažujme, že vzdálené těleso (ve vtažné soustavě, kdy těleso se pohybuje vůči nám jako klidovým pozorovatelům) vyzařuje (nebo odráží z okolí) paprsky v každý moment a z každého místa na svém povrchu. Obraz tělesa, který přijímáme jsou tak různé paprsky z různých částí tělesa přijatá v jednom okamžiku. Které to jsou?

U vzdalujícího tělesa paprsek vyslaný od odvrácené strany míjí přivrácenou stranu a bere tak do tandemu paprsek od přivrácené strany v okamžiku, kdy se těleso stačí posunout směrem od nás a výsledný obraz se tak zkrátí.

Z kolmého směru je vzdálenost stran od přijímačů stejná, obraz tělesa bude věrně kopírovat předlohu. (Při úhlech mezi to bude opět o Pythagorově větě).

U přibližujícího se tělesa paprsek vyslaný od odvrácené strany míjí přivrácenou stranu a bere tak do tandemu paprsek od přivrácené strany v okamžiku, kdy se těleso stačí posunout směrem k nám a výsledný obraz se tak prodlouží.

Když se nějaké těleso pohybuje ve směru pozorování, tak stejně vidíme jeho tvář nebo zadnici nezměněnou, žádné zkrácení nepozorujeme a celé to nějak pozbývá smyslu. Kdyby se těleso pohybovalo téměř světelnou rychlostí šikmo směrem k nám, mělo by mít tvar úsečky.

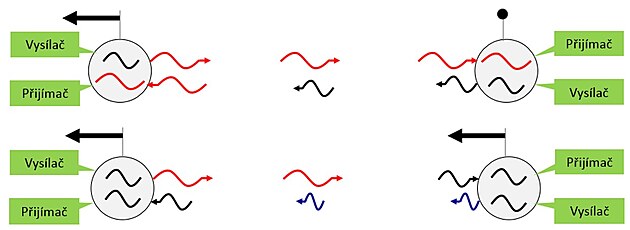
Při aktivním měření (obrázek níže), kdy by se nám vyslané paprsky nevrátily současně nebo při vysláním signálu z palubní desky uprostřed rakety k vysílačům na obou koncích bychom opět dostávaly jiné hodnoty.

 Jak už mnohého napadlo, fotony díky rychlosti c by neměly znát čas, tedy by se neměly rozpadat a měly by být věčné. Zanikat by měly jen srážkou s jinou částicí (například s elektronem), které by předaly svou mechanickou energii, rozvibrovaly by ji (tzv. by ji excitovaly). Jak je potom možné, že elektron může opět foton vyslat (vyrodit)?

Když se zamyslíme nad pozorovanou dilatací času u těžších částic (prodlužování poločasu rozpadu při vysokých rychlostech) nebo proměnami částic (rozpady), například anihilace při setkání elektronu a pozitronu, při níž se obě částice promění na fotony, nabízí se myšlenka, že těžší částice jsou složené z částic intermediálních (k nimž patří fotony) a že kvantová mechanika nefunguje podle představy mechanického kulečníku, kde částice si předávají energii pouze "drcáním" do sebe.  

Co jsou to fotony, v zásadě nikdo neví. Isaac Newton je nazval korpuskule, což se dá z latiny přeložit jako tělíska. Z Maxwellových rovnic vyplynulo, že světlo je EM vlnění. Na to Max Planck při řešení ultrafialové katastrofy vyzařování černého tělesa matematicky rozdělil EM vlnění do samostatných jednotek o určité energii. Tuto pomocnou konstrukci Albert Einstein svým objasněním fotoelektrického jevu opět vysvětil na samostatné částice. Nato Louis-Victor de Broglie vyslovil myšlenku, že částice se opět mohou chovat jako vlny a že jde o obecný jev náležející všem objektům.

Pozorovaná dualita částic (jednou se chovají jako vlny, podruhé jako samostatné částice) vedla k rámcové představě Teorie kvantového pole, kde částice jsou vlastně původně vlnami vyčnívajícími nad jeho hladinu, které se tímto vymezují.  Představa "rozbouřené" zvlněné plochy je samozřejmě pomocná. Pole je prostorové a částice jakoby vystupovaly ze skrytého paralelního světa. Z toho ihned plyne otázka po jeho podstatě a složení. Co se to tam vlastně vlní? Ve výhledu jsou temná hmota a temná energie, které mají zatím spíše podobu lidských slov. V každém případě ožívá myšlenka éteru a platforem jemnějších světla (EM vlnění) zbavených pout jeho rychlosti, které však mohou být pouze jednou z hranic na netušeně daleké cestě za pochopením podstaty nejpůvodněšího základního pole a energie (Goethe by řekl prasíly) jakož i původu gravitace.

Vezmeme-li v úvahu, že fotony reagují na gravitaci, přičemž gravitace je pojatá jako zakřivení prostoru aniž by se definovalo, co to vlastně prostor je, co se to vlastně zakřivuje, a zároveň se odstraní myšlenka éteru, pak se jedná o nejslabší ba přímo schizofrenní místo v díle Einsteinovy jím tak adorované představivosti.

Závěry STR jsou čistě matematické představy a jak víme příroda žádné matematické funkce nesleduje do extrémů. Jak by se tedy objekt choval při vysokých rychlostech nejlépe při 100% rychlosti světla?

Objekt s prostorovou strukturou má utvořené elektronové vazby (souhrnně) do všech stran. Zajímalo by mne (pomineme-li problematiku silné interakce, tj. interakci mezi kvarky v jádře), jak by se chovaly elektronové orbitaly? Jakým způsobem by se deformovaly, pokud by se deformovaly a co by to učinilo s celou strukturou? Můžeme zkusit různé možnosti:

1. Především Lorentzův faktor je odvozen z rozdílu kolmé a rovnoběžné dráhy interferometru a je vlastně vyjádřením poměru mezi krajními hodnotami rozměrů pohybujícího se objektu (umístění světelných hodin v raketě pod jiným úhlem než kolmým by sice měřilo jiné hodnoty, ale tyto by neměly pro výpočet smysl). Za chybnou považuji představu, že při 100% rychlosti světla by se objekt zcela zploštil. Poměr mezi drahami musí být nenulová hodnota vůči nenulové hodnotě byť limitně nulové, ale nikdy zcela nulové, neboť kdyby mezi dvěma elektrony ve směru letu byla nulová mezera, docházelo by k interakci okamžitě, zatím co v kolmém směru by to měl foton nekonečně daleko. Vznikl by tak objekt složený z bodů. Interakce tj. dosažení vedlejších částic v prostorové struktuře musí být v soustavě pohybujícího se objektu pro všechny fotony současná, což by bylo v tomto případě narušeno. 

2. Interakce by zanikly, elektrony by se rozpadly na fotony podobně jako při anihilaci.

3. Celé je to ptákovina, žádné (baryonové strukturované) objekty létat vysokými rychlostmi nebudou, neboť není síly, která by jim dodala takové zrychlení. I kdyby se naše dostatečně velký zdroj, při vysokých rychlostech by musela selhávat vlastní interakce pohonu, uvažujeme-li dosud známé možnosti reaktivního pohonu.

4. Doplňte si další možnosti, pokud nějaké znáte.

Mám za to, že skutečné chování velkých objektů ani nikdo exaktním způsobem nezjistí, neboť k dispozici jsou jen příchozí vyzařování objektů zpoza pro člověka nepřekročitelného obzoru a vědci, kteří si malují představy mezihvězdných letů jsou fantastové a pohádkáři, kteří marní svůj života čas, stejně jako ho teď marním já, když se tím zabývám. Člověk by měl pochopit svoji úlohu na Zemi, zabránit jejímu rozhodně ne nutnému předčasnému vybydlení, do toho vrazit čas, peníze a duševní síly, zároveň se poohlédnout po tom, jestli náhodou sám neobsahuje něco, co může putovat dál a rychleji, než jakékoli rakety, neboť např. tzv. dnes již nezpochybnitelné mimotělesné zážitky nikdo dostatečně důsledně nevysvětlil v rámci hrubé (vědecky uvažované) materie.

Příroda nám vytyčila život ve středních rychlostech. Vyšší rychlosti si nechala pro tkanivo forem, které kdybychom spatřovali (jako v Metrixu), pozbyl by náš svět oné harmonické ušlechtilé nádhery (Ta ovšem vlivem člověka také bere za své). Nic také nebrání tomu uvažovat o tkanivech světů jemnějších struktur s interakcemi rychlejších světla, které mohou prostupovat a být v základu světa naší matérie, ale také tvořit samostatné éteričtější světy. 

PS: Článek jsem nezamýšlel jako útok na STR, ale při bližším ohledání mi vytanuly v mysli určité obrazy, které jsem nedokázal dát v soulad (Samozřejmě důvodem může být má hloupost). Co lze říct s jistotou, že neúspěch Michelson-Morley experimentu byl jen důkazem chybnosti jedné zcela vymezené představy o éteru, nikoli neexistence éteru samotného. Je pravděpodobné, že stejně jako Newtonovská bude i Relativistická fyzika platná jen pro určitý okruh věcí a nové výhledy povedou k jakési éterové teorii, kde pravděpodobně slovo éter nebude použito a kde bude mít jiné vlastnosti, než ve zjednodušených a jednostranných představách minulých staletí.

Zdroje a poznámky:

Pro příklad s raketou jsem použil výtečné video učitele Michala Janovského ZDE, jež jsem našel v odkazech na WIKI, a které jsem doplnil o mezikroky, které učitel pro udržení stručnosti považuje pro studenta za samozřejmé. Pro lidi mého typu (již starší, pomalejší a nezběhlé v tématu nebo dlouho ze školy) jsem přesněji vymezil značení (s polopatickými indexy) a opakoval některé věci, u nichž hrozí, že je v proudu informací člověk neudrží v aktuální paměti (což chápu, že pro "rychlejší" mozky může být obtěžující).