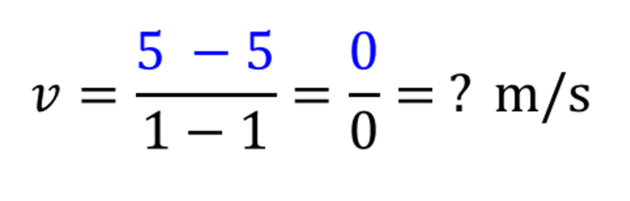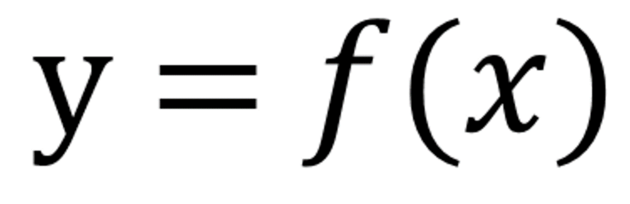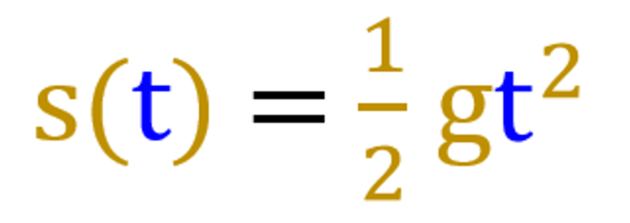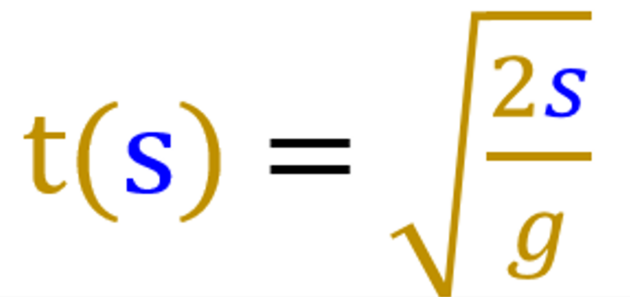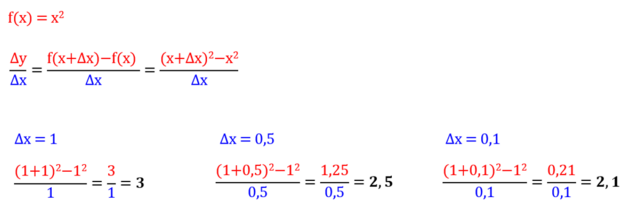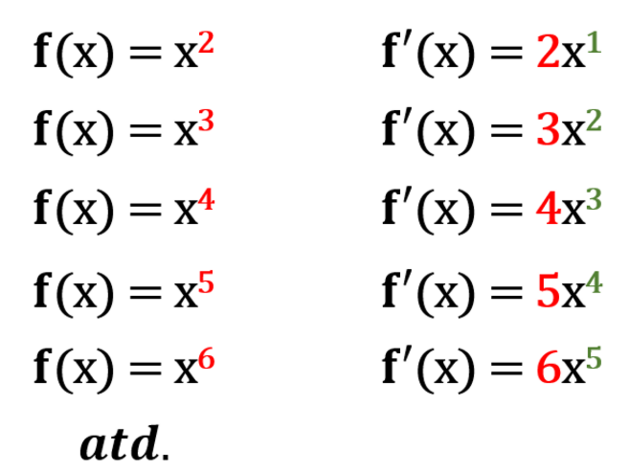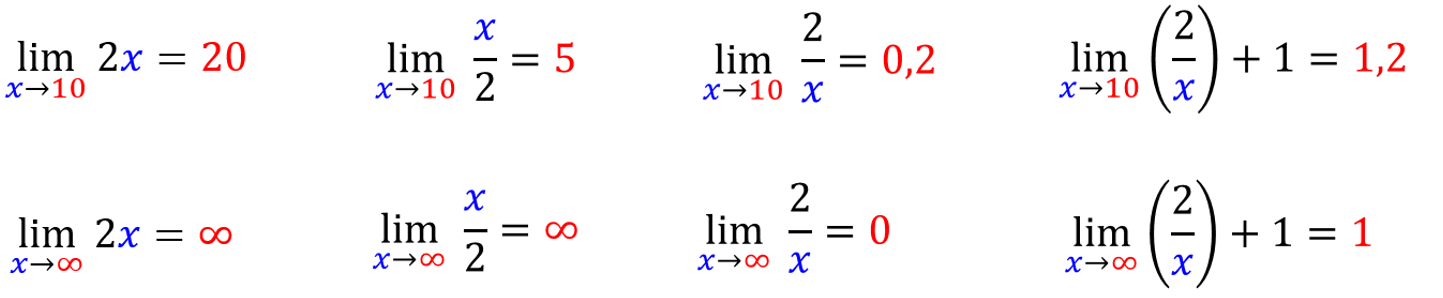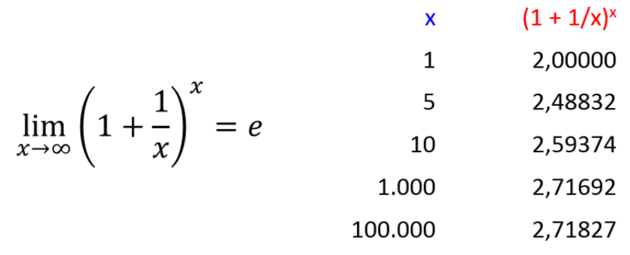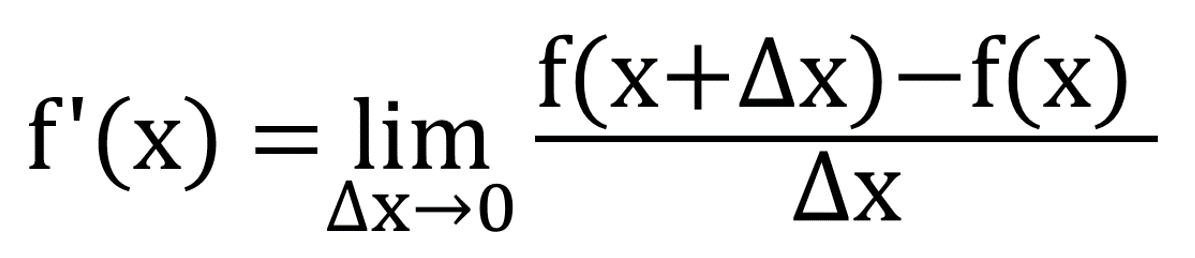Povídání o nekonečnu 6. - calculus

Při zamýšlení se nad nekonečností člověk nemůže nenarazit na infinitezimální kalkul, který má nekonečnost zanesenou již ve svém názvu.

Jde o látku poněkud komplikovanější, ale ne tak, aby její základy a podstatu nebyl schopen pochopit úplně každý. 

Patřím k těm pomalejším a nejsem v tom sám, což jsem si potvrdil malou soukromou anketou. Někdy mám pocit, že učitelé vykládají látku tak, jako by ji žáci či studenti už znali, jako by oni sami už dávno zapomněli na stav vlastní nevědomosti. Jsou to často drobnosti jako nedůslednost pojmenování "stavebních dílů" látky a jejich sestavení nebo vůbec mlhavé pojmy, které způsobují zásek a nedovolí putovat dál současně s výkladem a vlak pochopení tak beznadějně mizí za horizontem. Pozoruji, že se často k látce přistupuje bez počáteční opory v reálném světě, skočí se rovnou doprostřed vod formální abstraktnosti a nechá se na studentovi, zda to uplácá nebo se utopí, přitom právě znalost použití v běžném životě aktivuje podvědomé procesy zájmu. Vyloženě rozených  plavců je v každém oboru jen menší procento a není přece cílem školy pouze objevit talenty.

Po grafické stránce se mi zdá, že žijeme stále v době Gutenbergova knihtisku. Psychologie kognitivních procesů se dnes "využívá" spíš jen v reklamě. Symbolika barev, podklady a rozdělení na ploše, písma, obrázky, přirovnání atd., to je asi jenom pro prvňáčky. Otevřu stránky, kde mi garantují "zde to pochopíš" a pak následuje nepřehledná zeď písmen, ve které nenacházím žádné záchytné body pro zpětnou rychlou reaktualizaci zkoumaného.

Proto místo uvedení odkazů jsem si dovolil před svým povídáním na téma nekonečnosti v kalkulu přiblížit základy nutné k pochopení problematiky. Článek jsem viditelně rozdělil na části ÚVODNÍ PŘÍKLAD, FUNKCE, DERIVACE, GEOMETRICKÝ ROZBOR, LIMITA, PROBLÉM NEKONEČNOSTI, takže pro koho je látka samozřejmostí, může dané části rychle přeskočit k problému nekonečnosti, který se ale odvolává na geometrický rozbor. Téma samozřejmě nelze vsunout do jednoho článku, takže je zmíněno opravdu jen to nejzákladnější. Editor zdejšího webu není pro matematiku přizpůsoben, proto stati se zlomky a exponenty jsou vkládané jako obrázky, druh písma je k dispozici pouze jeden, takže jde jen o řídký odvar původně zamýšleného efektu.

Latinsko-anglicko-český jazykový hybrid (přidejme řečtinu a němčinu), který se usadil na pozici správce pojmů v našem mozkovém předivu, je ve skutečnosti programovým virem, který s lehkostí vytváří bludiště plné křivých zrcadel. Je to zmetek, který se nám snaží ukazovat v honosném hábitu. V obecné rovině je dnes už asi neléčitelný, pouze jednotlivci mohou proti němu bojovat a to jediným lékem - prostotou. Průzračnost pojmů je pro každé poznání věcí nejdůležitější a proto by měla být pro výuku věcí nejprvotnější. Právě tato věc byla Komenského původní hnací pohnutkou k jeho dílu. 

Pro jistotu malý slovníček původních významů:

Infinitezimální počet (kalkul) - počítání s nekonečně malými hodnotami.

derivace - odvození, vyvození

integrace - včlenění, zahrnutí

calculus - kamínek (oblázek kdysi používaný pro počítání; zde lze rovněž chápat jako zrnko písku na poušti).

ÚVODNÍ PŘÍKLAD

Svět kolem nás je v neustálém pohybu, vše se každým okamžikem mění. Některé pohyby mohou být velmi složité, jako například biologický růst, ale statistický růst populace je již mnohem jednodušší. Jednodušší mohou být také pohyby hmotných těles. Letadla, auta, vlaky putují svými drahami, tekutiny potrubími a nádržemi, elementární částice poli svých veličin, sportovní nářadí nebo kulky sviští vzduchem, z nebe padají meteority a z oken občas budoucí mrtvoly. Některé věci dopadnou a narazí vždy, některé jen občas, někdy to vydrží, někdy způsobí škodu. Některá tělesa během svého pohybu své parametry mění (třeba startující raketa svou hmotnost). Pro člověka je tedy nanejvýš zajímavé, aby znal stav veličin v daném okamžiku. 

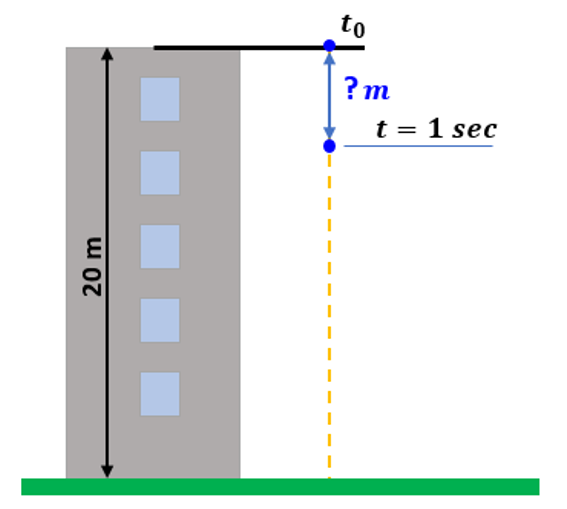
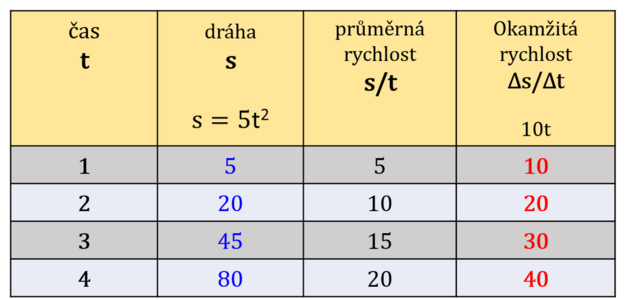
Podívejme se na kuriózní případ volného pádu. Na kraji střechy 20 m paneláku svačí hromosvodář Břéťa. Naneštěstí mu upadne jablko a zhruba tak po jedné sekundě trefí do hlavy z okna číhající drbnu Janáčkovou. Jablko hlavě pí Janáčkové předalo svou hybnost. Ta se vypočítá jako hmotnost krát rychlost. Nyní se zeptáme, jakou rychlostí letělo jablko volným pádem po uplynutí jedné sekundy.

Jenže ouha, toto je průměrná rychlost, ale my potřebujeme znát okamžitou rychlost přesně v bodě střetu jablka s hlavou pí Janáčkové.

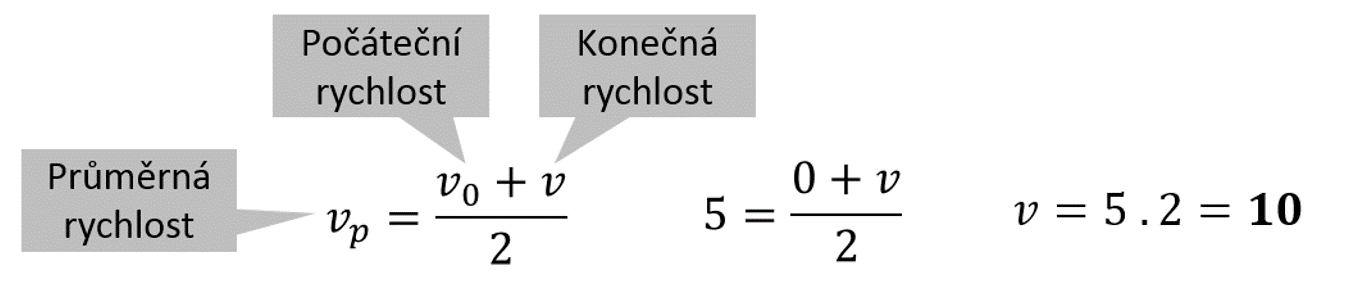
V tomto případě je sice možné použít jednoduchý výpočet, kde průměrná rychlost je aritmetický průměr počáteční a konečné okamžité rychlosti.  Počáteční známe, je nulová:

 Výsledek si však necháme pouze pro kontrolu našeho dalšího počítání pomocí kalkulu.

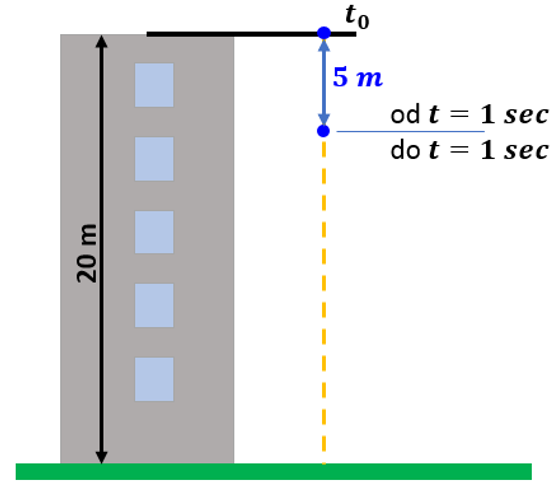
Nyní zkusíme okamžitou rychlost přímo v daném bodě (jablko-hlava).  Zkusíme začít i skončit v témže bodě, to znamená, že spočítáme rozdíl počáteční a konečné rychlosti v rozmezí bodu:

 V okamžiku, kdy přistane jablko pí Janáčkové na hlavu, má rychlost 10 metrů za sekundu. Břéťa měl sebou pláně kolem 100 g = 0.1 kg. Z toho plyne hybnost jako hmotnost tělesa krát jeho rychlost  p = m . v     0,1 . 10 = 1 kg . m/s. Nyní si vezměte 1 kg cukru nebo mouky a ze vzdálenosti 1 m se tak, aby vám tah rukou trval 1 s, udeřte do hlavy. (Případné pokusy zdokumentujte a klidně mi zašlete. Mohla by z toho být zajímavá galerie.) Řekněme, že pí Janáčková utrpěla spíš újmu psychickou než fyzickou.

O to tu ale neběží. Jde nám hlavně o ono odvození okamžité rychlosti ze vztahu dráhy a času.

Nyní si stejným postupem můžeme vypočítat okamžité rychlosti pro další časy trvání pádu a z hodnot si sestavit tabulku. (Samozřejmě pro pády z vyšších míst než naše budova). Vidíme, že okamžité rychlosti jsou vždy 10 krát vyšší než čas trvání pádu.

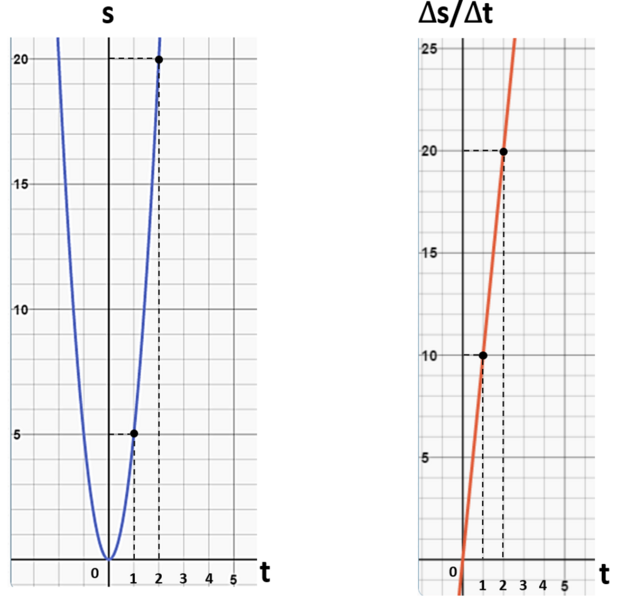
Rovněž si můžeme vytvořit graf. Vodorovná osa x jsou vstupní časy, které zadáváme. Svislá osa y jsou výstupní hodnoty, které ze vztahů dostáváme.

Vlevo (modrá parabola) výsledné dráhy generované vztahem 5t^2 - vstup je čas t, výstup dráha s. (Samozřejmě čas zde může být jen kladný, takže levou část paraboly nebereme v potaz).

Vpravo (červená přímka) vstup je ten samý čas, výstup jsou okamžité rychlosti jako poměry nekonečně malé dráhy delta s a nekonečně malého času delta t. Každý jednotlivý poměr pro každý jednotlivý vstup se nazývá derivací v bodě. Při znázornění všech bodů vznikne přímka, která je vyjádřením derivace celého vztahu.

Původní vztah můžeme nazvat funkcí a odvození všech bodů (které se nám zde zobrazuje jako přímka) pak derivací funkce. Po stažení rozdílu delta až k nule píšeme před proměnnou místo "trojúhelníčku" malé písmeno d, které nám říká, že jde o nekonečně malou (derivovanou) hodnotu.

Co je tedy derivace? Zadáváme-li na vstupu (teoreticky) kontinuálně hodnoty (například čas, který nepřetržitě běží v každém myslitelném okamžiku, bude vztah na výstupu generovat rovněž nepřetržité hodnoty, což se projeví jako nepřetržitá čára grafu. Když budeme chtít zachytit změnu v nějakém zvoleném okamžiku, tedy nejmenší možné poskočení hodnoty jak na vstupu tak i v projevu na výstupu, zjistíme, že nejsme schopni najít nejmenší možný úsek, protože úsek můžeme zmenšovat donekonečna. Můžeme ale při tomto zmenšování pozorovat, že hodnoty na vstupu a na výstupu se blíží ke zcela určitým číslům. Poměr čísla na výstupu ku číslu na vstupu je pak derivací v bodě. Pokud to samé zmenšení provedeme na každém bodě a výsledné poměry přiřadíme ke vstupním hodnotám, objevíme nový vztah, který je derivací celého původního vztahu .

Záměrně jsem se vyhýbal výrazu funkce, aby bylo vše ponecháno jen intuici. S formalismem obvykle na věci prosté padá mlha nesrozumitelnosti, prostě proto, že je vyumělkovaný. Nicméně u matematiky se bez něj neobejdeme. Takže teď probudíme ducha formalismu a poznatky si zobecníme za pomoci odborného slovíčkářství i lidové slovesnosti.

FUNKCE 

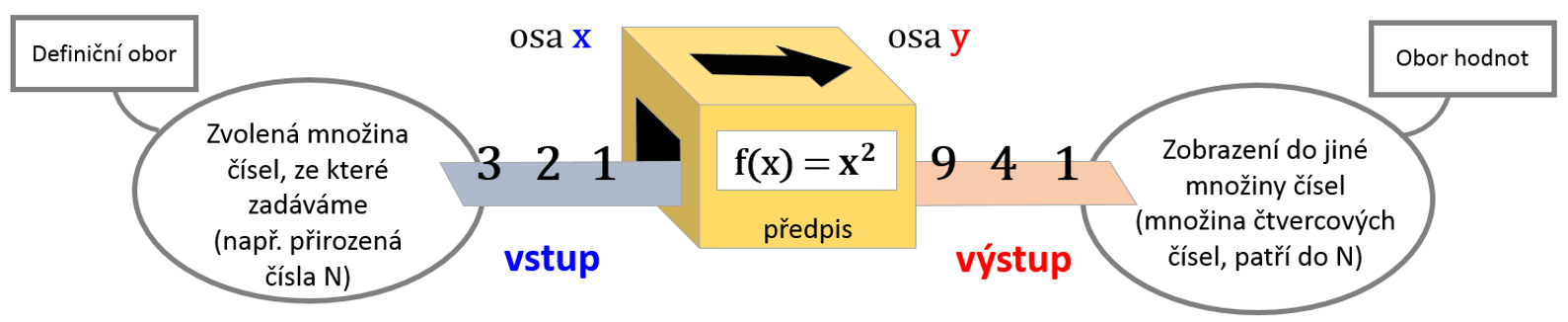
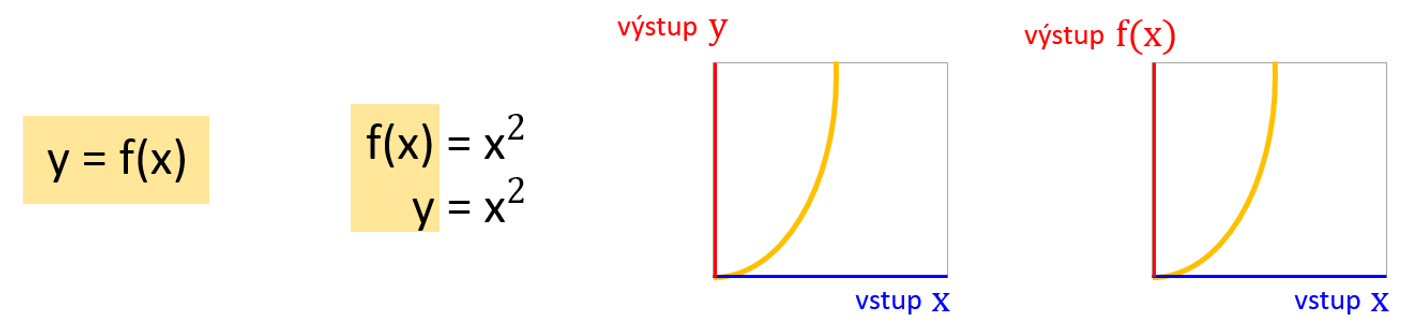
Co je to funkce? V matematice je to (jakákoli) obyčejná rovnice (například y=x^2), u které si určíme, která proměnná je vstupní a která výstupní. Funkcí si zvolenou rovnici právě pro záměrný způsob opakovaného použití v jednosměrném provozu pojmenoval pan Leibnitz.

Funkce vyjadřuje závislost jedné proměnné na jiné proměnné. Lze říct, že funkce je virtuální stroj, který vstupní hodnoty mění na výstupní podle zadání, které stroji předepíšeme. 

Jak bylo řečeno, máme tu dvě proměnné:

vstupní – nezávislá, tj. hodnota, kterou známe a zadáváme, má tedy charakter pevného tvrzení, proto ji říkáme argument.

výstupní – závislá, tj. hodnota, kterou potřebujeme zjistit, kterou nám funkce vyplivne, proto jí říkáme funkční hodnota.

Pozn.: Pojem funkce vznikl zhruba ve stejné době jako kalkulus. Pojem množin vznikl mnohem později pod tlakem potřeby vytvářet struktury či skupiny čísel podle jejich rozsahu a vlastností. Z pohledu teorie množin je pak funkce zobrazením jedné množiny do druhé.

Hodnota y se mění podle toho, jak se mění hodnota x. Můžeme říct, že y je funkcí měnící se podle x.

Právě tento základní obecný funkční předpis y = f(x) může začínajícího adepta hned zkraje mást. Zápis vlastně vyjadřuje rovnocennost výrazů ohledně výstupu. O vstupu hovoří vždy jen samotné x bez všeho dalšího. Po zadání nějakého skutečného úkolu se oba výrazy objeví na jedné straně. Oba zápisy jsou rovnocenné a vyjadřují funkci. Samozřejmě zápis s f(x) bez všeho dalšího nedává pochyb, že jde o zápis funkce.

Obě vyjádření se nazývají explicitní (česky vyjádřené, výslovné, jasné). Pak tu máme vyjádření implicitní (česky nezjevné, zahrnuté v něčem jiném) například, když vstup i výstup jsou na jedné straně rovnice a rovnají se nějaké konstantě, jako třeba x^2 - y = 0, což je pořád ta samá výše uvedená funkce. 

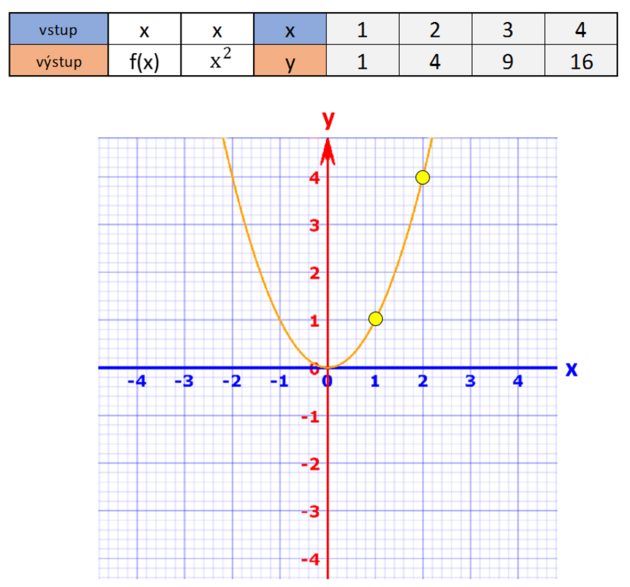
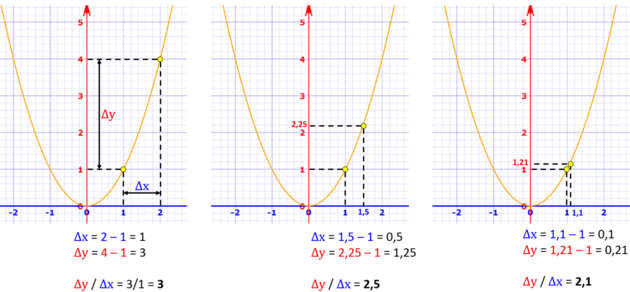
Z hodnot si můžeme sestavit tabulku nebo graf. Na grafu (který níže zobrazuje parabolickou křivku pro reálná čísla, nikoli jen pro přirozená čísla) lze vidět, jak se funkce mění. Zde, čím větší číslo na vstupu (modrá osa), tím větší poměr mezi výstupem a  vstupem, což se projevuje na rostoucím sklonu  křivky. Křivka je stále kolmější. 

Uvedené platí v případě, že známe vlastní proces funkce, tj. v nejčastěji v případě matematiky a fyziky nějaký vzorec. Pokud se jedná o neprobádanou oblast mapovanou pokusy, můžeme znát vstupní i výstupní hodnoty a funkci, tedy vlastní závislost z nich teprve zjišťovat – odvozovat.

Pojmenování funkce i proměnné může být jakékoliv např.  g(x) nebo k(n). Obecně nejčastěji píšeme f(x) nebo g(x).

Jakmile proměnnou určíme, tedy vložíme místo ní konstantu tj. číslo s určitou hodnotou, nazýváme vstup argumentem a výstup funkční hodnotou. 

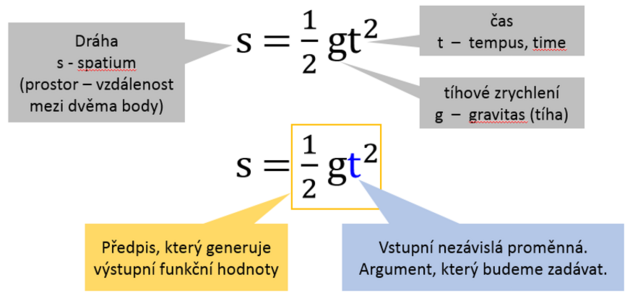
Každý fyzikální vzorec je vlastně zápisem funkce. Jde o to určit, co zvolíme jako vstup a co jako výstup. Zůstaneme u dráhy volného pádu.

 Ze vzorce pak můžeme vytvořit matematický formální zápis, který říká, že dráha je funkcí času, rozuměj dráha je funkce měnící se podle času. Prostě do závorky "vypíchneme" veličinu, kterou chceme zadávat.

V případě, že známe dráhu a chceme zjišťovat čas, pak si vzorec upravíme tak, aby čas byl funkcí dráhy (čas je funkce měnící se podle dráhy). 

DERIVACE 

Motto: Hledíme z výšky na autobus, jak projíždí serpentiny. Vidíme, že v každém okamžiku jízdy zatáčí. Autobus vyfotíme, necháme ho tak zamrznout v okamžiku. Pokud bychom odstranili vozovku, nevěděli bychom, že zatáčí. Viděli bychom pouze přímý směr. A právě tento směr by byl odvozením chování vozovky v daném přesném místě. 

Nyní si zobecníme poznatky z výše uvedeného příkladu. Skutečnost, že jsme jednu veličinu podle fyzikálního vztahu odvodili jako funkci jiné a pak pracovali matematicky jen s jednou, zobecňuje právě zápis y = f(x). Ve vzorci pak figuruje pouze x, což umožňuje další úpravy. Poměr obou rozdílů (výstupu a vstupu) pak můžeme formulovat do jednoduchého vzorce:

Jak jsme si řekli, derivace se týká okamžité změny, tedy změny během nekonečně malého intervalu (po dosazení veličiny třeba času, délky, plochy, intenzity atd.). K němu se dostaneme, když rozdíl budeme stále zmenšovat ke zvolenému bodu.

Držíme se stále funkce x^2. Zkusíme bod 1 (souřadnice: vstup 1 osa x, výstup 1 osa y (1^2=1)). Při neustálém zmenšování rozdílu delta x při zadávání do vzorce zjistíme, že se poměr stále více blíží k hodnotě 2. (níže je zobrazen rozdíl 1; 0,5; 0,1 pokračovat můžeme dále 0,001; 0,000001 atd).

Vyplníme vzorec funkcí x^2

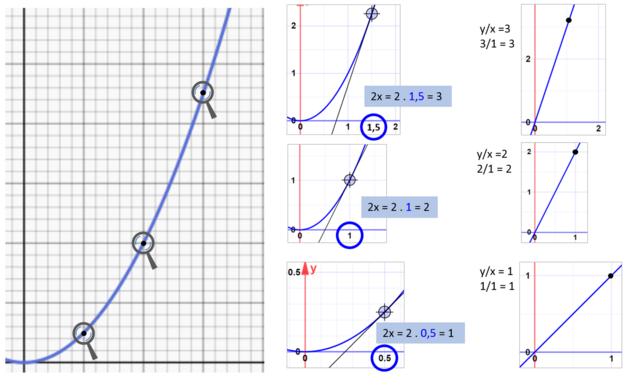
Pokud to samé "smrštění" provedeme v jakémkoli zvoleném bodě této funkce x^2, (kamkoli zapíchneme prst na žluté křivce) zjistíme, že výsledný poměr je vždy 2 krát větší, než vstupní hodnota x. Říkáme tedy, že derivace funkce rovná se 2x. 

Pokud bychom při výše uvedeném smršťování oba body na křivce protnuli přímkou, pojmenovali bychom tuto přímku "sečna". Při smrštění rozdílu téměř na nulu se ze sečny stane "tečna", neboť se dotýká křivky pouze v jednom bodě. Tato tečna (která jako každá přímka je vyjádřením lineární funkce), svým sklonem vyjadřuje poměr dy/dx v daném bodě, tedy vlastní derivaci.

Čím kolmější přímka, tím větší hodnota poměru, a tím "dramatičtější změna" funkce v daném bodě.

Jen ve zkratce. Pomocí derivace pak můžeme u funkce provádět různé analýzy, například najít její maxima či minima, tj. bod, kdy se stoupání obrací v klesání či obráceně, neboť v tomto bodě je sklon (poměr) nulový (vodorovný) a to aniž bychom si potřebovali tvořit graf. (obr. amplituda funkce sinus a vrchol kvadratické funkce výšky podle času při šikmém vrhu.

Ale vraťme se k vlastnímu vzorci. Provádět pokaždé přibližování by bylo poněkud nepraktické. Upravme tedy vzorec rovnou a vstupní rozdíl delta x ponechme nevyjádřený:

 Totéž můžeme provést s funkcí x^3

Při zvyšování exponentů nám ze vzorce poleze řada, ve které není těžké vypozorovat pravidlo:

Konstanta před proměnnou např. 6x^2, 10x^5 atd. nám říká, kolikrát je zúčastněna elementární funkce x^n, takže kolik funkcí, tolik derivací. Pokud derivace funkce x^2 je 2x, pak pro funkci 6x^2 je derivace 6 . 2x = 12x, pro 10x^5 je derivace 10 . 5x^4 = 50x^4.

Pravidlo:

Pravidlo platí i pro samotné x bez exponentu. To se dá zapsat jak s exponentem, tak i s konstantou před proměnnou, tj.  1x^1 (jedna iks na první). Snížíme-li exponent, dostaneme x^0 = 1. Konstantu před x násobíme exponentem, tedy jedničkou, takže

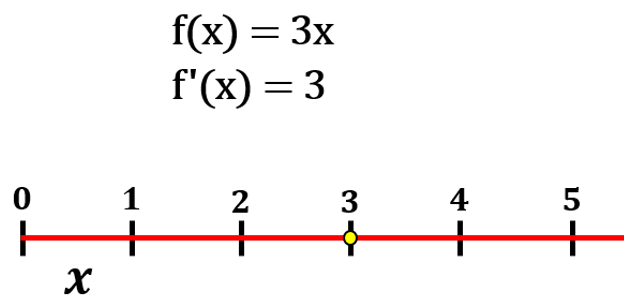
jestliže  f(x) = x,   pak f´(x) = 1

jestliže  f(x) = 2x, pak f´(x) = 2   atd.

Obrazný důkaz níže v geometrickém rozboru.

Ještě jednou pravidlo v obecném vzorci:

Samostatná konstanta bez x (například 2x + 1 nebo 25^5 - 3600) při derivaci odpadá, lépe řečeno její derivace se rovná nule, neboť se nemění, právě proto, že je to konstanta, jak slovo samo říká. (Česky by se jí mělo říkat "neměnná" jako opak "proměnné". Obrozenci to jaksi nepodchytili.) Například když předepíšeme funkci f(x) = 3, což můžeme, pak tato funkce ke každému číslu na vstupu vždy přiřadí číslo 3 na výstupu. Graf této funkce je pak vodorovná čára, a jak víme, míru změny určuje sklon.

Takže pro funkce x^2 + 5,  x^2 - 63 nebo  x^2 + 1000^6 bude derivace stále 2x. Na grafu vidíme, že konstanta nám funkci pouze posune v souřadnicích, ale na charakteristice jejího průběhu se nic nezmění. Je to stále ta samá parabola:

Dnes se pro derivaci využívají dva rovnocenné formální zápisy. Vlevo s čárkou (ef čárka iks rovná se dvě iks) a vpravo Leibnitzův zápis, který má funkci i derivaci v jednom řádku (dé iks na druhou podle (přes) dé iks rovná se dvě iks).

Nyní by se dalo pokračovat derivacemi dalších elementárních funkcí jako jsou například goniometrické, derivacemi vyšších řádů, integrálem, který je inverzní operací k derivaci podobně jako sčítání k odčítání nebo násobení k dělení, pravidly pro derivace složených funkcí, dále derivačními rovnicemi, atd., což pro svůj rozsah ani ve zkrácené formě nelze vtěsnat do jednoho článku. Základní princip je však stejný.

Také nebylo řečeno, že se dají derivovat  jen funkce spojité, tj. ty, co mají nepřerušenou čáru grafu. Derivace je vyjádřením rovnoměrné míry změny po celé délce funkce, proto musí být tato funkce harmonická a úplná. Svět kolem nás je spojitý a proto i jeho funkční vyjádření jeho dějů a veličin je většinou spojité.

GEOMETRICKÝ ROZBOR 

Skutečné pochopení přichází při obrazné představě. Vědět něco způsobem, že si pamatujeme zápis, by měl být středověký přežitek. Rovněž chápat něco pouze v číslech je jako se dívat na film a poslouchat pouze zvuk. Podíváme se tedy, co se to tam uvnitř vlastně děje.

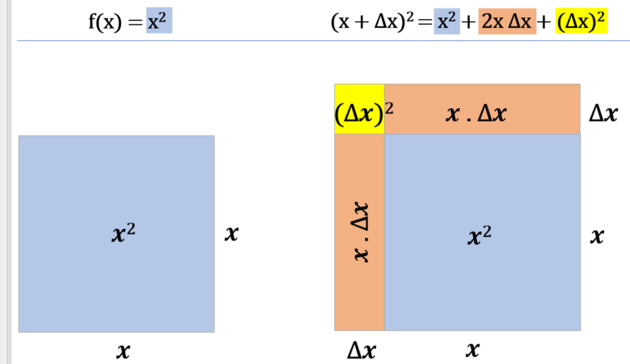
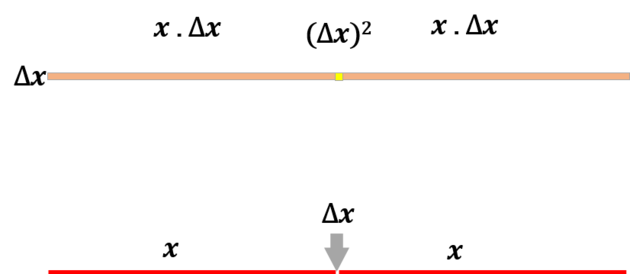
Začněme opět u funkce x^2. Když si prohlédneme úpravu derivačního vzorce, zjistíme, že kýžené 2x se nám objevilo při rozkladu závorky:

Obr. vlevo níže - funkce f(x)  

Obr. vpravo níže - funkce f(x+delta x)

Obr. vlevo níže - odečtením původní funkce nám zůstává jen rozdíl (naznačeno smršťování)

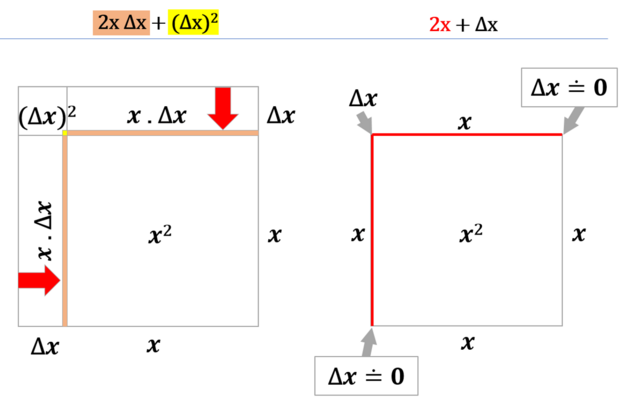
Obr. vpravo níže - Při smrštění k nule nám zůstanou jen ona kýžená 2x, tedy dvě úsečky o velikosti x. Rozdíl nemůžeme smrsknout až na nulu, protože by nám zmizel, ale můžeme se nekonečně k nule přibližovat. 

Je to právě hranice čtverce o velikosti 2x, která každým okamžikem při zvětšování čtverce (tj. při růstu funkce x^2) přibývá - způsobuje změnu:

Podobně si můžeme znázornit i funkci x^3. Vidíme, že při zvětšování krychle přibývají tři strany krychle, tedy tři čtverce, neboli 3x^2 (třikrát iks na druhou)

Při vyšších exponentech nebude představování už tak jednoduché. Pokud zůstaneme u symetrického zobrazení, tak funkce x^4 by měla mít své znázornění ve čtyřrozměrné hyperkrychli, tzv. teseraktu, jehož povrch tvoří 8 krychlí a ta by měla každým okamžikem přibývat o 4x^3 (čtyři iks na třetí), tedy o velikost 4 krychlí.

Pro vícerozměrné objekty si vytváříme pomocnou projekci v podobě posunutí 3D objektu. Ve skutečnosti si vyšší rozměry představit neumíme. Náš zrak umí vnímat pouze 2D (odhlédneme-li od mírného posunutí způsobené dvěma očima). Mozek si pak ze zkušenosti v čase umí ploché obrazy pomocí paměti přetvořit na 3D chápání. Lidská mysl si umí pouze představovat, tj. stavět před sebe. Vše vidí před sebou jako v divadle nebo v kině. Pouze je schopna si další obrazy paralelně vybavovat a tak vnímat souvislosti. Další hypotetické rozměry už chápe jen jako vztahy čísel podle odvozených pravidel. Pomocná zobrazení pak vyjadřují nějakou vybranou logickou vlastnost jako třeba propojení vrcholů za cenu ztráty vlastností ostatních (velikost úhlů atd.).

U symetrických zobrazení exponenciálních funkcí (x^n) jako jsou čtverec, krychle, atd. jsme viděli, že derivaci tvoří vždy polovina hranice objektu. Hraničních částí objektu je vždy dvojnásobek počtu rozměrů.

čtverec     2D          hranice     4  úsečky  

krychle     3D          hranice     6  stěn      

teserakt    4D          hranice     8  krychlí  

penterakt  5D          hranice    10 teseraktů  atd.

Proto nám krásně vychází, že exponent nad proměnou v původní funkci se rovná počtu proměnných nižšího řádu v derivaci. (nižší řád = nižší exponent)

Nyní ještě obrazný důkaz, proč konstanta, která se ve funkci nachází před x se při derivaci násobí exponentem. Například pětkrát iks na druhou.

Samostatné x (tj. lineární funkce x^1) geometricky vyjádříme úsečkou o délce x. Úsečka má jeden rozměr a její hranice tvoří dva krajní body. Poloviční hranicí, která se mění při doplňování různých hodnot za x, je právě jeden krajní bod. Kolikrát úsečku přidáme, tolikrát změníme hranici (posuneme bod). Proto derivace funkce a.x^1 (á krát iks na první) má hodnotu a.

LIMITA

Pokud do funkce strkáme čísla ze zvolené množiny či oboru (např. přirozená čísla 1, 2, 3 …), funkce na výstupu generuje číselnou řadu, která směřuje k určité hranici a této hranici říkáme limita (což znamená doslova hranice, mez)

Rozsah zadání (definiční obor) si můžeme přesně vymezit. Určíme-li pevné číslo, kde dosazování  končí (x šipka koncové číslo pod znakem limity), pak také na výstupu dostaneme pevnou hranici.

Necháme-li řadu volně běžet, zjistíme, že pokud se v předpisu funkce zvětšuje čitatel, řada přesahuje všechny meze směrem k nekonečnu, rozbíhá se, tj. diverguje a pokud se zvětšuje jmenovatel, zlomek se přibližuje k nule, a řada se sbíhá, tj. konverguje ke zcela určitému číslu.

U zápisu limity nebereme rovnítko doslova jako u rovnice. Pokud řada limity dosáhne, říkáme jí vlastní. Pokud se řada k limitě pouze přibližuje, říkáme jí nevlastní.

Známá iracionální čísla jsou vlastně limity nekonečných řad, například Eulerovo číslo (e = 2,7182818284590452353602874713527...)  generované funkcí (1 + 1/x)^x. Jeho přesnou hodnotu a vlastně ani přesnou limitu neznáme. Desetinný vývoj je nekonečný a bez opakujícího se vzoru. Hodnotu můžeme určit zaokrouhleně nebo tomuto vývoji dát pojmenování a symbol a pak můžeme napsat:

Jízlivá poznámka: Lidé vůbec spoustu věcí v tomto světě řeší zástupným pojmenováním. Nápis nebo značka je zcela určitá a takový má také budit dojem, i když se pod povrchem skrývá nejasnost a nejistota.

Správný zápis derivačního vzorce je rovněž ve formě limity. 

PROBLÉM NEKONEČNA

Vezměme opět graf funkce x^2. Jeho křivku, můžeme skládat z úseček, úsečky stále zmenšovat, tak, že se jejich délka bude přibližovat nule a bude tak simulovat bod. 

Křivka grafu funkce, je stejně jako každá čára nekonečně dělitelná a obsahuje v sobě nepostižitelné kontinuum. 

Limitní přibližování se k nule (či k jakékoli konvergentní hodnotě, tj. ke zcela určitému konečnému číslu) je obdobou nekonečného dělení úsečky, které můžeme chápat jako ten nejjednodušší fraktál. 

Když při derivaci dráhy podle času zmenšujeme rozdíl, je okamžitá hodnota vlastně průměrná hodnota na velmi malém intervalu. A protože si z matematického hlediska nedovolíme smrsknou rozdíl až nulu, považujeme hodnotu v bodě za hodnotu na nekonečně malé úsečce, kterou pak můžeme vyjádřit jako 1/nekonečno. Jenže okamžitá hodnota leží skutečně v bodě při rozdílu nula.

Při posouvání tečny po křivce grafu funkce můžeme na tomto bodě zastavit přesně. Tento bod nám odděluje část křivky před bodem a část za bodem Je skutečně bodem, tedy bezrozměrnou hranicí dvou intervalů. Můžeme se k němu dobrat i přes průměr a to úplně přesně. Pokud exponenciální funkci vyjádříme jako těleso, pak derivace je polovina jeho hranice (obalu), jak jsme si ukázali v geometrickém rozboru. Pokud budeme toto těleso zvětšovat a v určitém okamžiku ho vyfotíme (necháme zamrznout), pak bude tento obal vyjadřovat přesný stav v daném okamžiku (bod na tečně). Tuto hodnotu, pokud vyjadřuje nějakou veličinu, dál používáme jak hodnotu, se kterou operujeme. U funkce x^2 si pak z obou úseček můžeme vytvořit jednu.

Totéž můžeme udělat s okamžitou rychlostí volného pádu v = 10t uvedenou v úvodním příkladu. Úsečka pak slouží jako násobek ve vztahu pro výpočet hybnosti p = v . m a nikoho nezajímá její tloušťka.

O co tedy v kalkulu jde? O zjištění velikosti narůstající části hranice matematického objektu (pro x^2 úsečka, pro x^3 plocha). Z geometrie víme, že úsečka má nulovou tloušťku, plocha nulovou hloubku či výšku a že jsou to jen abstraktní objekty, které bez pozadí třírozměrných těles v realitě samostatně neexistují. Dobírat se k tloušťkám těchto objektů se pak může jevit jako slabomyslné počínání.

Je to podobné jako u funkce nespojité v bodě. Výstup při vložení jedničky není definovaný, protože nulou neumíme dělit. Můžeme se k jedničce pouze limitně přibližovat. Kdyby však tato funkce vyjadřovala tok nějaké přirozené veličiny, určitě by nám látka na dané hodnotě nezmizela.

Když zlomek upravíme, problém zmizí. A je to pořád ta samá funkce se stejným grafem.

Celý kalkulus je pouhá finta, jak obejít problém nedefinovaných operací s nulou a o vlastní nekonečnost tam vůbec nejde. Není to žádné dělení na nekonečně malé kousky při derivaci a jejich opětovné sčítání při integraci, ale pouze "důmyslné" získávání poměrů mezi obsahy a povrchy matematických objektů, které jsou zcela přesné. Zdá se být nepochopitelné, jak mohly na akademické půdě v této věci vzplanout rozepře. Nejsem žádný erudovaný matematik, ale již takto zpovzdálí se mi jeví, že kvůli zcela vedlejšímu problému vznikla především v teorii množil obrovská a odpudivá kupa formalismů ošetřující kdeco, kterou patrně žádný praktik nebere příliš v potaz.

Finito. Bídó, bídó, bídó.

POST SCRIPTUM

Geometrický rozbor jsem odnikud neopsal ani jsem na něj v dostupných stránkách nenarazil, prostě mě napadl.

Všechny obrázky jsem si vyrobil v aplikaci PowerPoint. Pouze podklad se silnicí a podklady grafů jsem použil stažené z netu.

Úvodní příklad jsem převzal a mírně přeobalil ze stránek MATH IS FUN, které jsou vzorovou ukázkou, jak by měl vypadat studijní web, který prozřetelně využívá v úvodu zmíněných pomůcek a poznatků. (Například tyrkysová barva podvědomě napomáhá jasnému zprostředkování informací především technického rázu). Je mým vroucím přáním, aby se našli učitelé, kteří by byli schopni něco takového vytvořit v českém jazyce.  Pár nití osnovy se dá citlivým uspořádáním přetvořit v přehledný vzor nebo se dá nedbalostí zašmodrchat v cucek. Pro mne osobně většina školních vědomostí nemá být cílem, ke kterému se namáhavě propracujeme, ale jen počáteční pomůckou na cestě za vyššími cíli života a rozhodně by tedy neměly spotřebovat životní síly v době rozkvětu. Přímost, přehlednost, prostota, jasnost, jednoduchost by měly stát v základu každého učení.

Důraz na obrazné chápání se může zdát příliš lidový či malicherný. Ale je to právě obraznost, která z jednostranného "vědce" dělá "filosofa" či "umělce". Jsou to právě obrazné představy, ze kterých se pak dají vyciťovat hlubší pojmy a jsou základem další invence. Ty pak umožňují při překračování vlastního oboru porovnáváním a slučováním vytvářet hlubší světový názor. Člověk se tak stává osobností s pevnou oporou v sobě, nikoli jen členem stáda s glejtem v kapse, který se pak klidně nechá strhnout k lecjaké lumpárně.

Člověk nikdy nic spěchem nezískal. Ke všemu, co povrchně přeběhl, se musel i mnohokrát vracet, než mu došla podstata věci. Má cenu pak vzdělání, které upřednostňuje kvantitu před kvalitou?