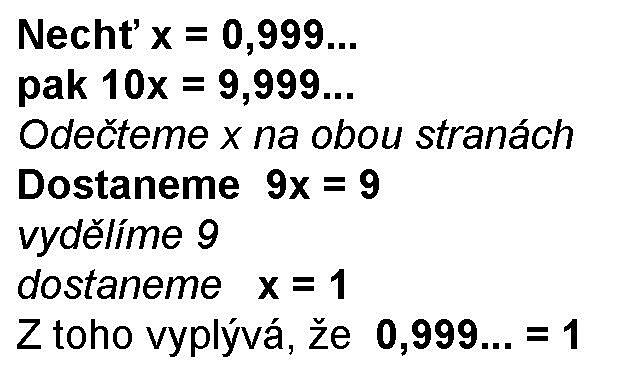Povídání o nekonečnu 1. díl - Nekonečný rozvoj

Své žvatlání o nekonečnu se hodí začít nekonečnem matematickým. A abych hned zkraje nezačal obecnou teorií proloženou filosofickými úvahami, vytáhnu z kapsy oblíbený silně ošuntělý příklad.

0,999... = 1. Nyní si ukážeme, že může jít o „člověkem“ posvěcený trik. Zkusíme-li stejnou rovnici s jakoukoliv zakončenou hodnotou, výsledkem bude nerovnost. Mohli bychom zadat číslo s řadou jakkoli dlouhou, ale pro názornost nám postačí tři desetinná místa, na zákonitosti se nic nezmění.

Vždy nám poslední devítka zmizí, což znamená, že vždy nám zůstane zbytek v podobě jedničky na posledním desetinném místě. VŽDY! Slyšíte to slovo. Vždy znamená věčnost, což jen jiný aspekt nekonečnosti. Operace probíhá donekonečna a nikdy nedoběhne, právě proto, že ta řada je nekonečná.Onen zbytek by se dal vyjádřit poněkud bizarním zápisem 0,000…1 (tři tečky = nekonečné opakování),nebo mnohem názorněji dosti známým matematickým objektem zvaným Cantorův prach. Jde o vývoj k nekonečně malému zbytku, který sám Cantor nazval diskontinuum.

Na prvním obrázku mizí vždy 5/9 původního obsahu (čtverce), na druhém obrázku mizí 1/3 (tyče, kterou můžeme brát jako úsečku). Tento útvar si upravíme tak, že odejmeme 9/10, takže vždy zůstane 1/10  tj.  0,1 předchozí hodnoty. (pro naše účely nehraje symetrie roli, je tedy jedno zda zbude 1/10 na jednom kraji původní úsečky nebo 2x 1/20 na obou krajích atd. Důležité je, že tam vždy NĚCO zbude, nikdy tam nezbude NIC.

Z toho vyplývá zápis rovnice 

1 – 0,999… = 0,000…1 nikoli 0 , jinak by cantorův prach musel končit na nule, čímž by nekonečný rozvoj musel být ukončen. To ale zavání přívlastkem "sporné".  

Ještě jednou, první obrázek je součet řady 1 + (-5/9) + (-20/81) + (-80/6561) + ... čitatel je od druhé pozice násoben 4, jmenovatel druhou mocninou.

Druhý obrázek je součet řady 1 + (-1/3) + (-2/9) + (-4/27) +... čitatel je násoben 2, jmenovatel 3

Náš uvažovaný prach je součtem řady 1 + (-9/10) + (-9/100) + (-9/1000) ... čitatel je od druhé pozice násoben 1, jmenovatel 10, což není nic jiného než odečtení 0,999... od jedničky.

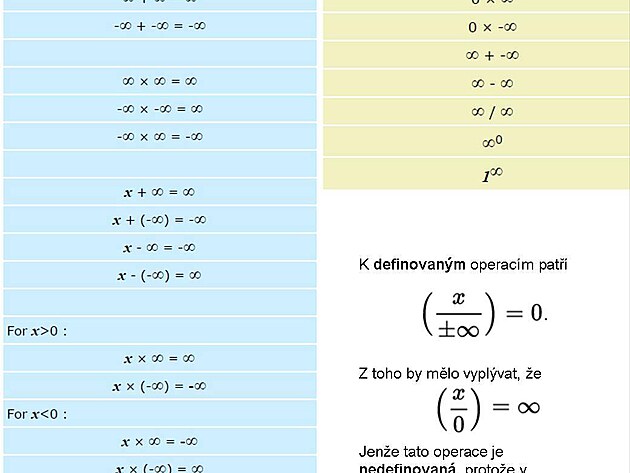
Problém je, že Cantorův prach není definovaný právě proto, že se zápisem této matematické entity si matematici nevědí rady. Není divu, 0,000…1 vypadá opravdu příšerně a jak vlastně s ní zacházet v kalkulu? Proto se stanovilo, že "jedna nekonečnina" nebo "x nekonečnin" se bude rovnat nule. (viz níže)

Opakuji z článku "oblíbená čísla": Nekonečnost ve skutečnosti není číslo, ale pouze idea, které byl pro určité potřeby statut čísla přidělen.

Pro mínus a plus nekonečno byla matematiky vytvořena kolonka "rozšířená reálná čísla". Čísla by se ale z tohoto hlediska spíše dala rozdělit na "pravá čísla" a "pseudo-čísla" či "polo-čísla" a od nich dále odvozené entity jako pseudomnožiny či polomnožiny.

Pravá čísla by byla čísla, se kterými lze provádět všechny standardní operace. Pseudo-čísla by byly útvary či idee, které v přesně stanovených podmínkách mohou zastupovat pozici čísla, ale pro které je nutné každou operaci zvlášť definovat, jak tomu ostatně už je. (nula, nekonečno).

Nulou nedělíme, je tedy víc než podivné, že nekonečnem můžeme. 

x / nekonečno = 0 se rovná tvrzení, že nejmenší prvkem kontinua je nula, čili, že jakákoli jiná hodnota je složena z nul, což je ekvivalentní k tvrzení, že vše existující je složeno z ničeho.Nebo je snad nekonečněkrát nula nějaké nenulové číslo?A tato operace je stěžejní částí důkazu: (uvedeném na idnes) 

Limita v nule je pak v posledním řádku zaměněna za nulu samotnou. Celé se to podobá kouzelnickému triku, nebo spíš práci zručného demagoga, který před vámi rozvíjí nádherný obraz smysluplné logiky vyvyšujíce exaktnost a v nestřežený okamžik vám naservíruje do hlavy jako samozřejmost sporný výraz, který vám pak nedá přemýšlet jinak, než jak on sám zamýšlel.

Problém je, že nekonečnost se nedá zkoumat exaktně, pokud exaktnost chápeme jako synonymum pro přesnost bez mlhavosti či neurčitosti, protože nekonečnost leží za obzorem našeho chápání natož praktického ověření, Vždy pro nás zůstane mysteriem, které si budeme pro praktické účely definovat nějakými uměle stanovenými axiomy.

Ještě je třeba vzít v úvahu tento nejpádnější součet. Vezmu zlomek 1/3, který mohu zapsat 0,333...  přičtu k němu 2/3 = 0,666... dostanu 1 (nebo mohu násobit 3 x 1/3). Racionální zápis 1/3 + 2/3 = 1 je nad slunce jasný, avšak 0,333... + 0,666... může platit jen tehdy, když budu počítat s tím, že v desetinném rozvoji se aktuálně nachází všech nekonečně mnoho trojek a šestek.

Rovněž z intuitivního hlediska to vypadá jako naprostá samozřejmost. Kdo to ale kdy aktuálně přehlédne a skutečně spočítá. Žádný člověk ani jím sestrojený sebelepší stroj to nikdy nedokáže. Buď se někde zasekne a zaokrouhlí nebo bude počítat do skonání věků. Není tedy v lidských schopnostech plně chápat a zapsat tento součet v desetinném tvaru, aby výsledek byl skutečně 1, tedy exaktně přesný. Kdykoli ve výpočtu figuruje neukončený podíl, se kterým se pracuje dál, výsledky jsou všelijaké, jenom ne přesné. O tom by mohli pracovníci s výpočetní technikou vyprávět.

Leckterý učitel má jistě zkušenost, že dosud vědomostmi nezatížená mysl studentova se vzpouzí proti tvrzení o rovnosti 0,999… a 1. Učitel by měl říci, že rovnost platí pouze pod podmínkou existence tzv. nekonečna aktuálního, což je věc do důsledku neověřitelná, a že existují i jiné náhledy s argumenty natolik pádnými, aby nemohly být šmahem ruky shozeny ze stolu jako nesmyslné, ale že se v současnosti nekonečno za takové považuje pro potřeby vytvoření axiomatické soustavy, tedy jakéhosi "matematického zákoníku práce". Ponechá tak studentovi otevřená vrátka a sám se nemusí bát, že by zhřešil proti matematickým pravdám.

 Závěrem: Pokud tedy v čísle 0,999... jsou devítky všechny, celá nekonečnost až do konce, a diskontinuum končí na nule, pak se 0,999... rovná 1.  O dilematu  Aktuální versus Potenciální nekonečno pojedná další článek..

PS: Nyní si mnohý může říct, že jsem demagog já, s těmi třetinami je to přece více než jasné. Udělejte si tedy ještě takový malý, dětsky prostý myšlenkový pokus. Zkuste najít hranici mezi čísly 0,333... a 0,666... Uvidíte dálnici vedoucí do hlubiny, po levé krajnici trojky, po pravé šestky. Potlačte pýchu a rozjeďte se. Jízda bude připomínat cestu do singularity černé díry. Pojedete tak dlouho, dokud se neunavíte, až si nakonec řeknete, tam někde v té mlze či tmě se ta dvě čísla spojí. Jak to ale víte? Nevíte, vy tomu věříte. Oni se ale přece nikdy nespojí, protože rozvoj nikdy nekončí. Stále uvidíte jen součet na devítku a nikdy na desítku. A matematický důkaz přece je, když něco ostře do sebe zapadne jako prdel na hrnec a následně pak otisk hrnce na prdeli na vlastní oči vidíte. Prostě nezůstane jakákoli šance o něčem pochybovat. A kdo může o nekonečnosti říct: "Já tam byl, já jsem to viděl". Mělo by se říct, že poměr jedna ku třem není v desetinné soustavě ostře definovatelný. Racionální 1/3 rovná se součtu nekonečné desetinné řady 0,3 + 0,03 + 0,003 +.... s limitou právě v jedné třetině. A limita není vlastní číslo.

Pozn.: Omlouvám se za poněkud bizarní zápisy, ale nástroj administrace článků není pro matematické symboly vybaven. Musí se vložit buďto jako obrázek, který ale nelze do textu umístit přesně nebo nezbývá než improvizovat.