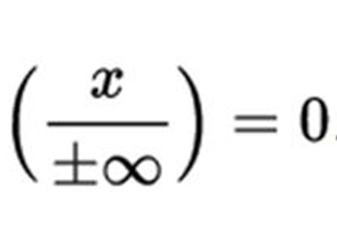Povídání o nekonečnu 2. - Spornost aktuálního nekonečna

Známe nekonečno celé nebo jsme vázáni naším obzorem? V předchozím díle bylo zatřeseno jistotou o rovnosti čísel 0,999... a 1. Nyní o tom, proč aktuální nekonečnost povždy zůstane pro člověka sporná.

Jsem jen buran, který selským rozumem proniká do světa matematiky podoben pralesnímu domorodci, který objevuje velkoměsto, Diví se stále více, že si lidé mohli život učinit tak komplikovaný, a naopak stále méně ho udivuje, že v něm nejsou šťastni. 

Vše existující známe nebo máme v představě v nějakém určitém nebo neurčitém počtu. Každou fyzikální veličinu - čas, frekvenci, svítivost atd., ale třeba také lidské rozechvění či rozčilení, pokud ho budeme jeho příznaky senzoricky měřit, můžeme převést na číselnou osu, tj. na délku. Geometrická představa délky je de facto jedinou veličinou, kterou se matematika v problematice nekonečna zabývá. Tuto délku pak můžeme donekonečna nastavovat, přidávat, přičítat  a vytvářet tak počet nekonečně velký nebo do nekonečna dělit, lámat a vytvářet tak počet nekonečně malý. (Skutečně můžeme? Kdo to umí?)

Základní problém nekonečna tedy můžeme z hlediska člověka jako pozorovatele zúžit na polopřímku, která začíná v nule a běží kamsi do nedohledna. Tomuto nedohlednu, to jest něčemu, co leží za naším obzorem říkáme nekonečno. Již nyní by prostě uvažující člověk (blahoslavený chudý v duchu) vyvodil závěr, že cokoliv, co leží za naším obzorem, nemůžeme dokonale znát, a tím pádem i s tím bezpečně či s jistotou pracovat. 

Nahlížení na nekonečno by se z průběhu dějin lidského bádání dalo pojmově rozdělit na nekonečno potencionální, aktuální a absolutní. Absolutní zatím ponechme stranou. Žhavým uhlíkem v srdcích myslitelů v průběhu dějin byla otázka, zda počítat  s nekonečnem potencionálním nebo aktuálním. Zabývání se historií může někomu (zvláště rutinním praktikům) připadat zbytečné, leč je nepopiratelným faktem, že objektivní posouzení přítomnosti není možné bez znalosti minulosti. Pokud se někde v minulosti vytvořil chybný pojem a na něm se stavělo dále, není jiné cesty, nežli se vrátit zpět, pojem opravit a pak vše vystavět znovu, jinak každá další přestavba bude mít v sobě zakotven kolaps. Důsledky nedodržování tohoto univerzálního pravidla dnes vidíme ve většině lidského počínání.

Podívejme se na původní problém, který vedl k pozdějším "novověkým" úvahám a sporům o nekonečno, lépe řečeno o aktuálně nekonečné množiny, neboť o řadách čísel na číselné ose bylo později uvažováno jako o množinách prvků. Nutno dodat,že problém se řešil již daleko dříve, ale zde dostal zřetelnou podobu v historii vědy skrze výjimečnou a medializovanou osobnost.

Jde o tzv. problém čtvercových čísel uvedený Galileo Galileem ve spisu Rozprava a Matematické Důkazy o Dvou Nových vědách.
Otázka zní: Je více přirozených nebo čtvercových čísel?

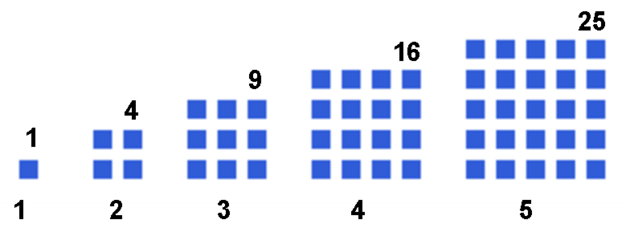
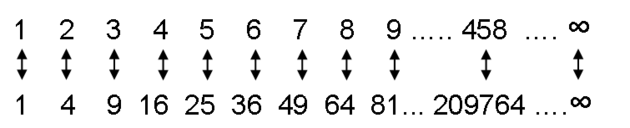
Přirozená čísla jsou 1, 2, 3, 4, … Každé přirozené číslo mohu vynásobit sebou samým, vzniknou tak druhé mocniny čili čtverce 1, 4, 9, 16, …

Opačně vzato mohu říct, že číslo 2 je kořenem čtverce 4, číslo 3 je kořenem čtverce 9 atd.

Pozn.: Čeští jazykovědci dali kořenu název odmocnina, jako opaku k mocnině. V angličtině se používá slovo "root" - kořen, stejně jako dříve v antických a středověkých spisech a dnes ve všech ostatních jazycích včetně slovanských, s výjimkou slovenštiny, která po léta úpěla po nadvládou češtiny. Opět jedna "hloupá" jazyková výjimka, která nás odděluje o jednoty vyjadřování pojmů.

Zatímco přirozená čísla nacházíme na ose směrem do nekonečna ve stále stejných rozestupech, čtvercových čísel rapidně ubývá.

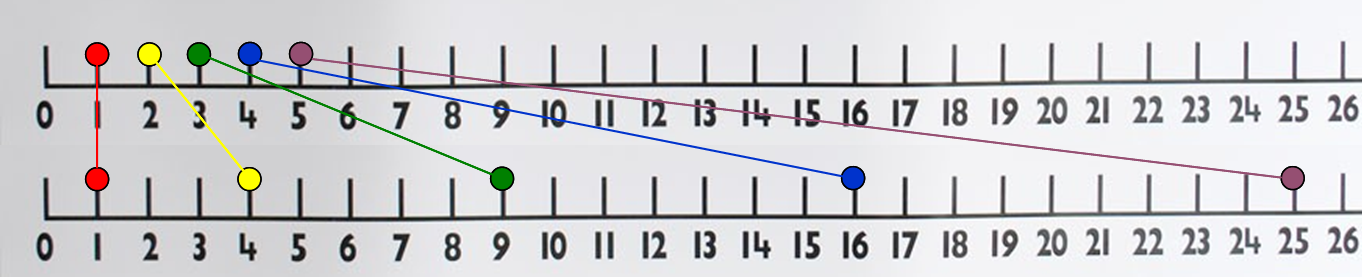
První úvaha by mohla být, že čtvercových čísel je méně. Avšak je zde potíž, ke každému přirozenému číslu 1, 2, 3. ... mohu přiřadit (dát do uspořádané dvojice) jeho druhou mocninu neboli čtvercové číslo 1, 4, 9, ... , přičemž u obou druhů čísel máme možnost přidávat donekonečna, takže z tohoto pohledu je jich stejně - stejně nekonečně mnoho. A právě ono tvoření uspořádaných dvojic neboli tzv. bijekce je vlastně úhelným kamenem i kamenem úrazu celého problému.

Už nyní bych rád poukázal na samotný jazyk jako na nástroj logiky a zprostředkovatele obrazných představ. Pokud řeknu "máme možnost přidávat donekonečna" je tím vyjádřena potence. Pokud řeknu "je jich stejně nekonečně mnoho" použiji matematický existenční kvantifikátor "je", který hovoří v aktuálním bezčasí věčné přítomnosti. Současná matematika má právě ono bezčasí zakotveno ve svém "predikátovém kalkulu", tj. v uzpůsobené vyhraněné logice jazyka. Náhled je takový, že v matematických principech se nic nevyvíjí, vše je od věčnosti dáno, člověk pouze v čase jednotlivé principy odhaluje a popisuje. Každá operace tedy probíhá v nulovém čase, všechny díly jsou kdykoli po ruce stejně jako celek a my je pro počítání pouze necháme vystoupit do popředí. To je zajisté samozřejmé a správné, pokud se jedná o cokoli jakkoli velkého, ale ohraničeného. Začneme-li ale uvažovat v neukončených rozměrech, začíná vyvstávat řada problémů a sporů, tedy alespoň pro člověka, který samostatně přemýšlí a rozvinul trochu soustředěné představivosti. 

Galileo k problému dodává: "Nekonečně je jak všech čísel, čtverců i kořenů. Není žádná veličina, která by zachytila počet všech čtverců a která by byla menší než ta, která by zachytila počet všech čísel."
Před tím ještě podotýká: "Náš rozum je konečný, následkem čehož na vše myslíme tak, jako by to bylo konečné a to i tehdy, když hovoříme o nekonečnu. To nám ovšem nepřináší žádný užitek, neboť přívlastky větší, menší nebo stejný nejsou na nekonečno použitelné."

Ve stejném spisu je uveden další problém: Je více bodů na kratší nebo delší úsečce. Opět první, co člověka napadne, je, že samozřejmě na té delší. Galileo však říká: Není jich ani více ani méně, ba ani stejně. Na obou je jich nekonečně.
A má pravdu, neboť jak víme z Euklidových Základů bod je to, co nemá rozměr. Bod je pouze hranice intervalu (interval = odcamcať pocamcať), a vlastní číslo není bod, nýbrž právě interval od nuly po daný bod, tedy úsečka. 

Galileo prozíravě varuje před nesmyslností porovnávání nekonečností, avšak jak to bývá, žáci učí své žáky, ti rádi sledují moderní směry a snadno zapomínají vracet se k základům, které často položili lidé se skutečně zjasnělým celostním myšlením. Galileo nekonečno připouští, ale jen jako potenciální, nikoli aktuální. Uvádí: „Máme čáru 20 palců, to neznamená, že je složena z 20 jednopalcových čar, ale že ji lze na těch to 20 čar rozložit. Těch 20 jednopalcových čar je v potenci, až na ně čáru rozdělíme, budou v aktu.

Galileo zde k problému přistupuje z "lidského hlediska" - tedy někoho, kdo nahlíží, měří a počítá v posloupnosti událostí, tedy v čase, což má své oprávnění - o tom později.

Naopak současná moderní matematika se chová jako Bůh, který dokáže aktuálně přehlédnout nekonečno celé. Pracuje tedy s nekonečnem aktuálním, tj. předstírá, že všechno nekonečné dělení nebo nekonečné nastavování je již provedeno. Připouští tak existenci nekonečně velkých nebo nekonečně malých těles, a vlastně tvrdí, že je dokáže spatřovat. Těleso jak víme, je definováno právě svými hranicemi. V geometrii kontinuální tělesa jako krychle nebo koule by ztratila svou identitu a vůbec smysl. Pokud bychom chtěli prostor vyplnit nějakým "bublinkovým materiálem", byla by identita takových těles sice definována jejich vzorem tvaru a rozložení dutých míst, avšak operace s takovýmito celými tělesy by byly poněkud problematické, nehledě na smysluplnost. v zásadě bychom se dostali zpět k přímce či polopřímce, která je pro lidskou mysl věcí stejně nepochopitelnou. 

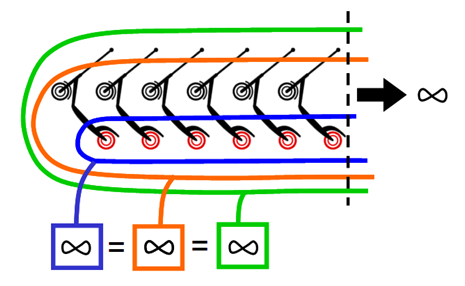
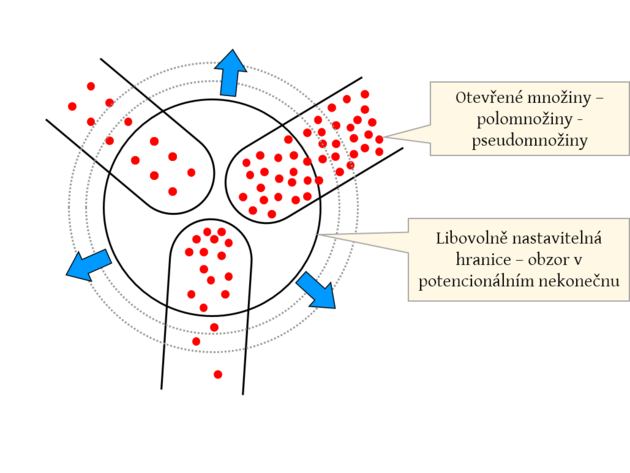
V zárodku "aktualizace" nekonečna stojí pražský rodák matematik, logik, katolický kněz a filozof Bernard Bolzano, který ve svém spisu Paradoxy Nekonečna (paragraf20) uvádí svůj objev, že v případě nekonečných množin může být podmnožina stejně velká jako množina do které patří, přičemž v této množině mohou být i jiné prvky, které do uvedené podmnožiny nepatří. Například máme nekonečnou řadu koloběžek. Každá koloběžka má dvě stejná kola, jedno přední, jedno zadní. Máme tedy množinu všech kol a pak máme podmnožinu třeba všech zadních kol.

Pokud začneme vzájemně (bijektivně) zobrazovat, tj. budeme do jedné řady pokládat kola z množiny všech kol a do druhé řady z podmnožiny všech zadních kol a protože řada koloběžek nikde nekončí, budou obě řady "stejně nekonečně" dlouhé, a proto obě množiny stejně velké. A vůbec nevadí, že podle prosté úvahy musí všech kol být dvakrát více než kol zadních už podstaty stavby koloběžky.

Tento příklad lze převést například na množinu celých čísel (kladná + záporná) a množinu celých kladných čísel, což jsou vlastně čísla přirozená.
Na obrázku jsem záměrně nedokončil "kruhy" znázorňující množinu s prvky (o tom dále). 

Bolzano byl kritizován, že si nevytvořil jednotnou terminologii, se kterou by se dalo přehledně pracovat, čímž se jeho práce stala pro druhé odtažitou. To však nebylo případem druhé osobnosti, kterou byl německý matematik Georg Cantor, který se myšlenky bijekce zarputile chytil a „obohatil“ Teorii množin o mnoho dalších pojmů nekonečnosti. Začal zdůvodňovat, která nekonečna jsou větší či menší nebo který číselný obor je větší či menší (například reálných čísel je více než přirozených čísel) nebo dokázal, že množina všech podmnožin je větší než původní množina, což se příčí axiomům Euklidových Základů („Část je menší než celek“ a „Co se překrývá, rovno jest“) a tím i zdravému rozumu. Začal řešit bizarní sebou ustanovené úkoly jako je spočetnost množin číselných oborů, o jejichž praktičnosti se dá vskutku pochybovat, ale které zřejmě na jeho současníky právě pro svou bizarnost působily zvláštním kouzlem.

Na příklad dokázal, že bodů je na dvou různě velkých úsečkách "stejně nekonečně mnoho". Srovnej Cantorův výrok s Galileovým: "Přívlastky větší, menší nebo stejný nejsou na nekonečno použitelné". Nyní si dovolím říct, že Cantorův výrok je slovní podvod - čirá demagogie. Vždyť bod je pouze pomocné označení, které nemá žádnou hodnotu, je to pouze kóta, okraj úsečky bez vlastní "mocnosti". Sčítat body je nesmyslná operace jako sčítat třeba kulaté trojúhelníky, reálně přece žádné neexistují. Člověk se chytil do pasti vlastní řeči, protože je zvyklý čemukoli, co má pojmenování, přidělit jakousi "substanci", se kterou lze nějak manipulovat. Celé je to podpořeno Bolzanovými představami "Pravd o sobě", které dávají právo na počitatelnost všemu, co se urodí v lidské hlavě.

Pokud chci porovnávat kontinua dvou různých úseček, je nevhodné zvolit ke sčítání body jako okraje intervalů. Tvrzení, že je jich stejně, je věcí matoucí právě pro spornost aktuálního nekonečna. Přibližování ke kontinuu se provádí dělením úsečky. Stále můžeme dělit a nikdy k nějakým bodům nedorazíme. Vždy uvidíme jen úsečky ohraničené dvěma body. Vždy!!! Tvrzení, že mezi dvěma reálnými čísly je rozdíl právě jednoho bodu, je nesmyslné. Bod má nulovou hodnotu a znamenalo by to shodnost těchto dvou čísel. Určením minimální úsečky jako atomu kontinua, o což se někteří matematici snažili, by kontinuum přestalo být kontinuem. Vidíte to před sebou, chápat kontinuum jako aktuální je nad lidské schopnosti a každé tvrzení v tomto ohledu bude zákonitě sporné. Tvrzení, že na dvou různých úsečkách je stejně bodů je tvrzení nesmyslné, stejně jako je nesmyslné tvrdit, že úsečka se skládá z bodů. Vždyť bod má nulovou délku a jakékoli nenulové číslo by muselo vznikat součtem nul.

0 + 0 + 0 +....= (x > 0)  NONSENS

Pokud se na kontinuum podíváme jako na nekonečno potenciální, uvidíme, že se pro to náramně hodí. Ona "možnost dělit do nekonečna" je právě onou potencí, která nepožaduje dojít do konce, ale jen tak daleko, kolik potřebujeme. Z tohoto pohledu můžeme určit jakkoli malou úsečku, kterou použijeme pro porovnání dvou různě velkých úseček, například 1/G (G - Grahamovo číslo, jehož velikost nikdo nikdy nespočítá), a výsledek bude, že těchto úseček bude právě tolikrát více, kolikrát je delší úsečka větší . Nepřipadá vám, že jsme se vrátili do světa zdravého rozumu?

Mám obavu, že pan Cantor vytvořil pseudoproblém, na který se nechali chytit generace matematiků.

Oba dva autoři Bolzano i Cantor byly silně věřící a ve svých pracích se opírali o své teologické představy, což v zásadě i velká část myslitelů do té doby. Existencí aktuálního nekonečna jakož i jsoucností nebo nejsoucností jiných vlastností předmětů vědy se zabývali již osobnosti typu Tomáš Akvinský, kterým i přes ovlivnění již tehdy zkřivenými představami křesťanské kosmologie nelze upřít naprostou brilantnost uvažování. S podivem je třeba říci, že někteří tito poctiví teologové nepřipouštěli, že u Boha jsou možné věci sporné (Bůh je omezen sám sebou, tedy sebou stanovenými zákony), na rozdíl od náboženských dogmatiků, kteří připustí i ten největší nesmysl a to z dětinské představy o absolutní Boží všemohoucnosti. Velká část těchto myslitelů byla ohledně tohoto tématu váhavá, až se tu náhle objevil pan Cantor, který s jistotou rozhodl, že Bůh zná všechny čísla až do nekonečna, že je aktuálně nazírá, proto musí existovat i množina všech čísel jako cosi uzavřeného a dokončeného, což dávalo oprávnění považovat nekonečno za aktuální – tedy jako cele uskutečněné. 

Následovníci fascinováni některými výsledky začali Cantorovu teorii množin čím dál více považovat za samozřejmost, stavět na ní dále a dnes v čase totálního vědeckého materialismu se už ani vlastně neví, že fundament celé současné matematiky je vystavěn na osobním teologickém důkazu. Cantorovi nemůžeme upřít jeho geniální invenci a především způsob, jak dosavadní poznatky matematiky popsal, srovnal a zpřehlednil, podobně jako to učinil Karel Marx v ekonomice (pojmy jako pracovní prostředky, pracovní předměty nebo pracovní síla byly prozíravě zvolené, vhodné pro vědeckou práci), avšak to neznamená, že musíme přijmout všechny jeho závěry.

V představě aktuálního nekonečna spolu poměřujeme nekonečné množiny řad čísel, jako bychom je měli po ruce celé (v uzavřené ohrádce). Operace mezi takovýmito množinami se pak musí jevit jako sčítání hrušek a jablek. (Výsledkem je vždy 1 kus kompotu).

Většina operací s aktuálním nekonečnem se dá zaměnit za násobení jedničkou, přičemž jedničku jako výsledek zpětně dostat nesmíte.

Jedinou "připuštěnou" operací, ve které dostanete jiný výsledek než 1 kompot  je tento:

Slovy: Cokoli vezmeme a vydělíme to něčím tak velkým, že to svět neviděl, výsledkem bude úplný kulový. Teď vážně, i když je to jen obměna toho, co bylo řečeno v 1. díle a  výše, zkusme se na toto dělení podívat maličko z jiného úhlu.

Představme si samuraje stojícího před velkou dýní. Nejdříve rozsekne dýni jedním úderem vejpůl. Dělit dvěma znamená dělit na dva díly a provést operaci odseknutí – odečtení jednou. Další dýni rozsekne na čtyři díly. Sekne třikrát. Pokud má dýni dělit jedničkou, neprovede žádnou operaci odečtení. Dýně zůstane celá. Operací je vždy o jednu méně než dílů. To samé platí pro násobení jako opakované přidávání. Nyní samuraj dostane úkol provést dělení nulou, což znamená provést  méně než žádnou operaci, což je samozřejmě neproveditelné zadání. Dělit nulou nedává smysl. Matematici tomu kulantně říkají, že je nedefinované.

Samuraj nanejvýš může dostat rozkaz zachovat formálnost úkonu a tak máchne mečem do vzduchu, což znamená, že provedl jakou si pseudo-operaci oddělení prázdné množiny. Prázdná množina není nic jiného než pomocný konstrukt pro zachování formy zápisu či zobrazení. Můžeme tedy napsat 1/1 = 1 + 0.

Potom dostane za úkol rozsekat dýni na tolik kousků, aby výsledek byl nula. Samuraj bude mlátit dýni na kaši do věčnosti a teď se zeptám, může dýně zmizet úplně? Podle současné matematiky ano. Tato operace je definovaná právě díky představě aktuálního nekonečna, tj. že nekonečné dělení někdo provedl celé, že věčnost scvrkl do nulového okamžiku, že to co je neukončené, de facto ukončil.

Já vám říkám, dýně nezmizí, samuraj bude dělit a zase jen dělit a nikdy neskončí, protože dělení je nekonečné, což není nic jiného než problém Cantorova prachu uvedený v 1. díle. Výsledkem žádného dělení nemůže být nula, (můžeme to brát jako zákon zachování energie, čili nějaké entity nebo potence, čehokoli co má nenulovou hodnotu). 

Opačně když skladník Goliáš Hemerka bude přidávat krabici ke krabici, nikdy hromada nebude po ruce celá. Nekonečno, které je aktuálně po ruce je náboženským pohádkám podobná dětinská představa vypadlá z Cantorova mozku. Sousloví "celá nekonečnost"  má podobný smysl jako kadit v kulaté místnosti do rohu. Jedno slovo ze své podstaty vylučuje druhé. Děti si z podobných sousloví dělají šprťouchlata.  V nejlepším případě by se dalo použít jako protimluv do Shakespearových Sonetů. 

Celé to proběhlo tak, že Jirka vzal kouzelnou hůlku, máchl do vzduchu, řekl Infinitum aktuális a bylo. Nadšení kolegové s hrachem snědli i broky, postavili piedestal pro hrnec s vtipnou kaší a po kanonizaci si už jen tak někdo nedovolil něco namítat. Noví studenti, ti jsou rádi, když se učení nabiflují, dostanou zápočty, protože pro život je především potřeba titul, nikoli nepřízeň neomylných profesorů. Učení je hodně a tak ani není čas se něčím zabývat hlouběji a (nebesa nedej) prostě. A potom, když už nějaký čas zbude, tak už naučené sami učí druhé nebo řeší jiné praktické problémy a to už se dostávají do kruhu ...rutina, zvyk, jistoty, pohoda, peníze, prestiž atd.

Z celé věci mám čím dál více dojem, že celá aktuálně infinitní matematika, je matematika Harryho Pottera, která s prominutím vypláchla mozek několika generacím matematiků a zkřivila všem pochopitelnou prostotu uloženou do zákonů čísel.

Článek je už velmi dlouhý, takže zde jen ukázka představy množin v potencionálním nekonečnu. Více příště.